已知定义在正实数集上的函数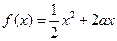 ,
,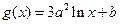 ,其中
,其中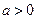 . 设两曲线
. 设两曲线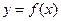 ,
,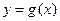 有公共点,且在该点处的切线相同.(I)用
有公共点,且在该点处的切线相同.(I)用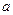 表示
表示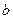 ;(II)求证:
;(II)求证: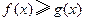 (
(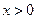 ).
).
(12分) 已知函数
 -4
-4 (a∈N﹡).(Ⅰ)若函数
(a∈N﹡).(Ⅰ)若函数 在(1,+∞)上是增函数,求a的值;(Ⅱ)在(Ⅰ)的条件下,若关于x的方程
在(1,+∞)上是增函数,求a的值;(Ⅱ)在(Ⅰ)的条件下,若关于x的方程 在区间[1,e]上恰有一个实根,求实数b的取值范围.
在区间[1,e]上恰有一个实根,求实数b的取值范围.
(13分) 如图1, 在直角梯形 中,
中, 



 ,把△
,把△ 沿对角线
沿对角线 折起后
折起后
如图2所示(点 记为点
记为点 ), 点
), 点 在平面
在平面
上的正投影 落在线段
落在线段 上,连接
上,连接 .
.
(Ⅰ)求直线 与平面
与平面 所成的角的大小;
所成的角的大小;
(Ⅱ)求二面角 的大小的余弦值.
的大小的余弦值.
图1图2
(13分) 某次国际象棋友谊赛在中国队和乌克兰队之间举行,比赛采用积分制,比赛规则规定赢一局得2分,平一局得1分,输一局得0分,根据以往战况,每局中国队赢的概率为 ,乌克兰队赢的概率为
,乌克兰队赢的概率为 ,且每局比赛输赢互不影响.若中国队第n局的得分记为
,且每局比赛输赢互不影响.若中国队第n局的得分记为 ,令
,令 .(1)求
.(1)求 的概率;(2)若规定:当其中一方的积分达到或超过4分时,比赛不再继续,否则,继续进行.设随机变量
的概率;(2)若规定:当其中一方的积分达到或超过4分时,比赛不再继续,否则,继续进行.设随机变量 表示此次比赛共进行的局数,求
表示此次比赛共进行的局数,求 的分布列及数学期望.
的分布列及数学期望.
(13分) 如图,在四边形ABCD中,AB=3,AD=BC=CD=2,A=60°。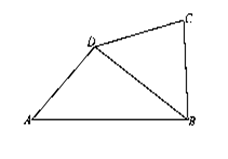
(1)求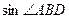 的值;(2)求
的值;(2)求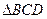 的面积。
的面积。
(本小题满分14分)
在数列
(1)求证: ;
;
(2)求证: ;
;
(3)若