(13分) 某次国际象棋友谊赛在中国队和乌克兰队之间举行,比赛采用积分制,比赛规则规定赢一局得2分,平一局得1分,输一局得0分,根据以往战况,每局中国队赢的概率为 ,乌克兰队赢的概率为
,乌克兰队赢的概率为 ,且每局比赛输赢互不影响.若中国队第n局的得分记为
,且每局比赛输赢互不影响.若中国队第n局的得分记为 ,令
,令 .(1)求
.(1)求 的概率;(2)若规定:当其中一方的积分达到或超过4分时,比赛不再继续,否则,继续进行.设随机变量
的概率;(2)若规定:当其中一方的积分达到或超过4分时,比赛不再继续,否则,继续进行.设随机变量 表示此次比赛共进行的局数,求
表示此次比赛共进行的局数,求 的分布列及数学期望.
的分布列及数学期望.
(本小题满分14分)一块边长为10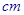 的正方形铁片按如图所示的阴影部分裁下,然后用余下的四个全等的等腰三角形加工成一个正四棱锥形容器,试建立容器的容积
的正方形铁片按如图所示的阴影部分裁下,然后用余下的四个全等的等腰三角形加工成一个正四棱锥形容器,试建立容器的容积 与
与 的函数关系式,并求出函数的定义域.
的函数关系式,并求出函数的定义域.
(本小题满分14分)
如图所示,在长方体 中,AB=AD=1,AA1=2,M是棱CC1的中点
中,AB=AD=1,AA1=2,M是棱CC1的中点
(Ⅰ)求异面直线A1M和C1D1所成的角的正切值;
(Ⅱ)证明:平面ABM⊥平面A1B1M1
(本小题满分14分)
已知圆C: ,是否存在斜率为1的直线l,使l被圆C截得的弦AB为直径的圆过原点,若存在,求出直线l的方程;若不存在说明理由。
,是否存在斜率为1的直线l,使l被圆C截得的弦AB为直径的圆过原点,若存在,求出直线l的方程;若不存在说明理由。
(本小题14分)已知圆C的圆心在直线 上,且与直线
上,且与直线 相切,被直线
相切,被直线 截得的弦长为
截得的弦长为 ,求圆C的方程.
,求圆C的方程.
(本小题满分12分)
为了比较注射A,B两种药物后产生的皮肤疱疹的面积,选200只家兔做实验,将这200只家兔随机地分成两组。每组100只,其中一组注射药物A,另一组注射药物B。下表1和表2分别是注射药物A和药物B后的实验结果。(疱疹面积单位: )
)
完成下面频率分布直方图,并比较注射两种药物后疱疹面积的中位数大小;