.已知定义在R上的二次函数 满足
满足 ,且
,且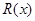 的最小值为0,函数
的最小值为0,函数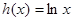 ,又函数
,又函数 。
。
(I)求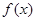 的单调区间; (II)当
的单调区间; (II)当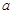 ≤
≤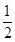 时,若
时,若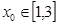 ,求
,求 的最小值;
的最小值;
(III)若二次函数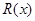 图象过(4,2)点,对于给定的函数
图象过(4,2)点,对于给定的函数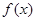 图象上的点A(
图象上的点A( ),
),
当 时,探求函数
时,探求函数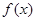 图象上是否存在点
图象上是否存在点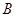 (
( )(
)(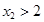 ),使
),使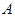 、
、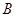 连线平行于
连线平行于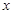 轴,并说明理由。(参考数据:e=2.71828…)
轴,并说明理由。(参考数据:e=2.71828…)
设函数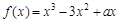
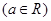 .
.
(1)当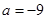 时,求函数
时,求函数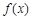 的极大值;
的极大值;
(2)若函数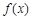 的图象与函数
的图象与函数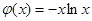 的图象有三个不同的交点,求
的图象有三个不同的交点,求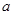 的取值范围;
的取值范围;
(3)设 ,当
,当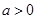 时,求函数
时,求函数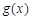 的单调减区间.
的单调减区间.
如图所示,在平面直角坐标系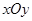 中,设椭圆
中,设椭圆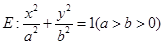 ,其中
,其中 ,过椭圆
,过椭圆 内一点
内一点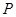
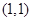 的两条直线分别与椭圆交于点
的两条直线分别与椭圆交于点 和
和 ,且满足
,且满足 ,
,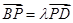 ,其中
,其中 为正常数. 当点
为正常数. 当点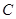 恰为椭圆的右顶点时,对应的
恰为椭圆的右顶点时,对应的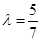 .
.
(1)求椭圆 的离心率;
的离心率;
(2)求 与
与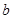 的值;
的值;
(3)当 变化时,
变化时,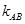 是否为定值?若是,请求出此定值;若不是,请说明理由.
是否为定值?若是,请求出此定值;若不是,请说明理由.
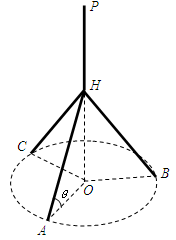
如图所示,某人想制造一个支架,它由四根金属杆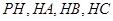 构成,其底端三点
构成,其底端三点 均匀地固定在半径为
均匀地固定在半径为 的圆
的圆 上(圆
上(圆 在地面上),
在地面上), 三点相异且共线,
三点相异且共线,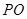 与地面垂直. 现要求点
与地面垂直. 现要求点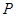 到地面的距离恰为
到地面的距离恰为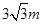 ,记用料总长为
,记用料总长为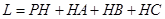 ,设
,设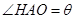 .
.
(1)试将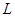 表示为
表示为 的函数,并注明定义域;
的函数,并注明定义域;
(2)当 的正弦值是多少时,用料最省?
的正弦值是多少时,用料最省?
设函数 .
.
(1)用反证法证明:函数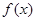 不可能为偶函数;
不可能为偶函数;
(2)求证:函数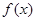 在
在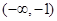 上单调递减的充要条件是
上单调递减的充要条件是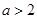 .
.
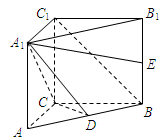
如图,在直三棱柱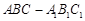 中,
中,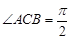 ,
,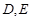 分别是
分别是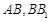 的中点,且
的中点,且
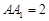 .
.
(1)求直线 与
与 所成角的大小;
所成角的大小;
(2)求直线 与平面
与平面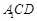 所成角的正弦值.
所成角的正弦值.