要将两种厚度、材质相同，大小不同的钢板截成
、
、
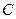三种规格的成品．每
张钢板可同时截得三种规格的块数如下表：
| 成品规格类型 钢板类型 |
A规格 |
B规格 |
C规格 |
| 第一种钢板 |
1 |
2 |
1 |
| 第二种钢板 |
1 |
1 |
3 |
每张钢板的面积：第一张为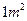
，第二张为
．今需要、、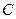三种规格的成品
各为12、15、27块．则两种钢板各截多少张，可得所需三种规格的成品，且使所用钢板的面积最少？
在三角形ABC中，三内角满足A＋C＝2B，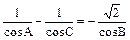
，求cos
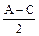的值
解关于x的不等式：loga(x2－x－2)＞loga(x－
)＋1(a＞0，a≠1)
已知：如图，射线OA为y=2x(x>0)，射线OB为y= –2x(x>0)，动点P（x, y）在
的内部，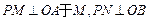
于N，四边形ONPM的面积为2..
（I）动点P的纵坐标y是其横坐标x的函数，求这个函数y=f(x)的解析式；
（II）确定y=f(x)的定义域.
 |
已知水渠在过水断面面积为定值的情况下，过水湿周越小，其流量越大.现有以下两种设计，如图：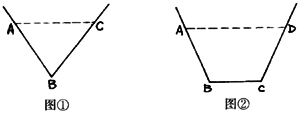
图①的过水断面为等腰△ABC，AB=BC，过水湿周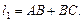
图②的过水断面为等腰梯形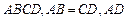
∥
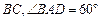，过水湿周
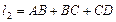.若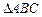
与梯形ABCD的面积都为S，
（I）分别求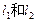
的最小值；
（II）为使流量最大，给出最佳设计方案.
已知等差数列{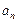
}的公差为d，等比数列{
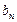}的公比为q，且，
（
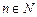），若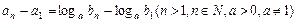
，求a的取值.