某工厂拟建一座平面图(如下图)为矩形且面积为200平方米的三级污水处理池，由于地形限制，长、宽都不能超过16米，如果池外周壁建造单价为每米400元，中间两条隔墙建造单价为每米248元，池底建造单价为每平方米80元(池壁厚度忽略不计，且池无盖).
(1)写出总造价y(元)与污水处理池长x(米)的函数关系式，并指出其定义域.
(2)求污水处理池的长和宽各为多少时，污水处理池的总造价最低？并求最低总造价. 
设a＝(－1,1)，b＝(4,3)，c＝(5，－2)
(1)求证：a与b不共线，并求a与b的夹角的余弦值；
(2)求c在a方向上的投影；
(3)求λ1和λ2，使c＝λ1a＋λ2b.
已知A(－1,0)，B(0,2)，C(－3,1)，且·＝5，2＝10.
(1)求D点的坐标；
(2)若D的横坐标小于零，试用，表示
已知函数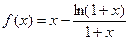
(Ⅰ)求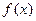
的最小值
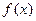（Ⅱ）若在区间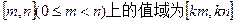
,试求k的取值范围.
设椭圆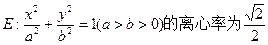
，
已知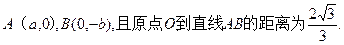
(Ⅰ)求椭圆E的方程；
（Ⅱ）已知过点M(1,0)的直线交椭圆E于C,D两点，若存在动点N，使得直线NC,NM,ND的斜率依次成等差数列，试确定点N的轨迹方程.
在直角梯形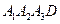
中，
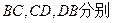将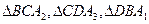
翻折上去恰好使
(Ⅰ) 求证：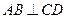
;
（Ⅱ）已知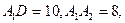
试求：
（1）四面体ABCD内切球的表面积；
（2）二面角
的余弦值.