某人手中有5张扑克牌,其中2张为不同花色的2,3张为不同花色的A,有5次出牌机会,每次只能出一种点数的牌但张数不限,此人有多少种不同的出牌方法?
求函数 在
在 上的最大值,其中
上的最大值,其中
设函数f(x)=ax2+8x+3 a<0
a<0 。对于给定的负数a,有一个最大的正数l(a),使得在整个区间[0,l(a)]上,不等式|f(x)|≤5恒成立.问:a为何值时,l(a)最大?求出这个最大的l(a),证明你的结论.
。对于给定的负数a,有一个最大的正数l(a),使得在整个区间[0,l(a)]上,不等式|f(x)|≤5恒成立.问:a为何值时,l(a)最大?求出这个最大的l(a),证明你的结论.
设{a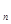 }是由正数组成的等比数列,S
}是由正数组成的等比数列,S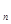 是前n项和。
是前n项和。
①证明: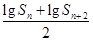 <lgS
<lgS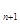 ;
;
②是否存在常数c>0,使得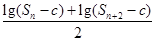 =lg(S
=lg(S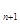 -c)成立?并证明结论。
-c)成立?并证明结论。
求证平行于三棱锥的两条相对棱的平面截三棱锥所得的截面是平行四边形.
已知:如图,三棱锥S—ABC,SC∥截面EFGH,AB∥截面EFGH.
求证:截面EFGH是平行四边形.
关于x的方程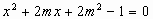 至少有1个负实数根,求实数m的取值范围。
至少有1个负实数根,求实数m的取值范围。