已知f(x)=ax3+bx2+cx(a≠0)在x=±1时取得极值,且f(1)=-1.
(1)试求常数a、b、c的值;
(2)试判断x=±1是函数的极小值还是极大值,并说明理由.
设数列 的前
的前 项和为
项和为 ,且
,且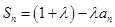 ,其中
,其中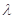 为常数,且
为常数,且
(Ⅰ)证明:数列 是等比数列;
是等比数列;
(Ⅱ)设数列 的公比
的公比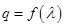 ,数列
,数列 满足
满足 ,
, (
( 求数列
求数列 的通项公式;
的通项公式;
(Ⅲ)设 ,
,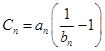 ,数列
,数列 的前
的前 项和为
项和为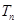
某校从参加高一年级期末考试的学生中抽出60名学生,并统计了他们的物理成绩(成绩均为整数且满分为100分),把其中不低于50分的分成五段 ,
, …
… 后画出如下部分频率分布直方图.观察图形的信息,回答下列问题:
后画出如下部分频率分布直方图.观察图形的信息,回答下列问题:
(Ⅰ)求出物理成绩低于50分的学生人数;
(Ⅱ)估计这次考试物理学科及格率(60分及以上为及格)
(Ⅲ)从物理成绩不及格的学生中选两人,求他们成绩至少有一个不低于50分的概率.
在 中,角A,B,C所对的边分别为a,b,c,且
中,角A,B,C所对的边分别为a,b,c,且
(1)求角B的大小;
(2)若 ,且
,且 ,求
,求 的最小值.
的最小值.
已知二次函数 对任意
对任意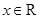 ,都有
,都有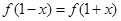 成立,设向量
成立,设向量 (sinx,2),
(sinx,2),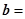 (2sinx,
(2sinx,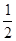 ),
), (cos2x,1),
(cos2x,1), (1,2),当
(1,2),当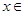 [0,
[0,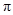 ]时,求不等式f(
]时,求不等式f(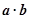 )>f(
)>f(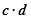 )的解集.
)的解集.
已知圆 ,
, 是直线
是直线 上的动点,
上的动点, 、
、 与圆
与圆 相切,切点分别为点
相切,切点分别为点 、
、 .
.
(1)若点 的坐标为
的坐标为 ,求切线
,求切线 、
、 的方程;
的方程;
(2)若点 的坐标为
的坐标为 ,求直线
,求直线 的方程.
的方程.