某果园要将一批水果用汽车从所在城市甲运至销售商所在城市乙。已知从城市甲到城市乙只有两条公路,且运费由果园承担。若果园恰能在约定日期(×月×日)将水果送到,则销售商一次性支付给果园20万元;若在约定日期前送到,每提前一天销售商将多支付给果园1万元。若在约定日期后运到,每
迟到一天销售商将少支付给果园l万元。为保证水果新鲜度,汽车只能在约定日期的前两天出发,且只能选择其中的一条公路运送水果。已知下表内的信息:
(1)记汽车走公路1时果园获得的毛利润为 (单位:万元),求
(单位:万元),求 的分布列和数学期望
的分布列和数学期望 ;
;
(2)假设你是果园的决策者,你选择哪条公路运送水果有可能让果园获得的毛利润更多?
注:毛利润=销售商支付给果园的费用-运费
已知直线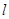 的参数方程为:
的参数方程为: (
( 为参数),曲线
为参数),曲线 的极坐标方程为:
的极坐标方程为: .
.
(1)以极点为原点,极轴为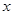 轴正半轴,建立直角坐标系,求曲线
轴正半轴,建立直角坐标系,求曲线 的直角坐标方程;
的直角坐标方程;
(2)若直线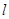 被曲线
被曲线 截得的弦长为
截得的弦长为 ,求
,求 的值.
的值.
设函数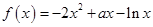 (
(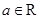 ),
),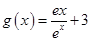 .
.
(1)若函数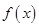 在定义域内单调递减,求实数
在定义域内单调递减,求实数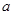 的取值范围;
的取值范围;
(2)若对任意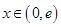 ,都有唯一的
,都有唯一的 ,使得
,使得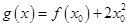 成立,求实数
成立,求实数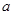 的取值范围.
的取值范围.
已知直线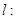
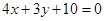 ,半径为
,半径为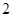 的圆
的圆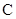 与
与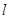 相切,圆心
相切,圆心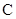 在
在 轴上且在直线
轴上且在直线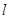 的右上方.
的右上方.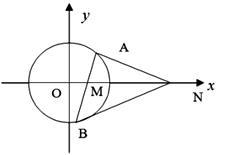
(1)求圆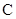 的方程;
的方程;
(2)过点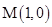 的直线与圆
的直线与圆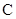 交于
交于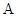 ,
,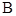 两点(
两点(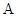 在
在 轴上方),问在
轴上方),问在 轴正半轴上是否存在定点
轴正半轴上是否存在定点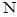 ,使得
,使得 轴平分
轴平分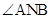 ?若存在,请求出点
?若存在,请求出点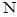 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
如图,在直角梯形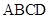 中,
中, ,
,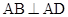 ,且
,且 .现以
.现以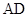 为一边向梯形外作矩形
为一边向梯形外作矩形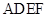 ,然后沿边
,然后沿边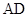 将矩形
将矩形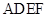 翻折,使平面
翻折,使平面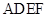 与平面
与平面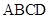 垂直.
垂直.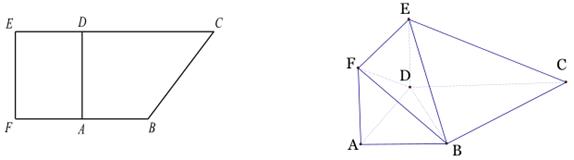
(1)求证: 平面
平面 ;
;
(2)若点 到平面
到平面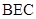 的距离为
的距离为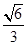 ,求三棱锥
,求三棱锥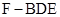 的体积.
的体积.
已知等比数列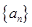 满足
满足 ,且
,且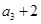 是
是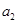 ,
,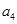 的等差数列.
的等差数列.
(1)求数列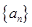 的通项公式;
的通项公式;
(2)若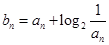 ,
,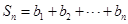 ,求使
,求使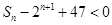 成立的
成立的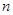 的最小值.
的最小值.