(本小题满分12分)下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量x(吨)与相应的生产能耗Y(吨标准煤)的几组对照数据
| x |
3 |
4 |
5 |
6 |
| y |
2.5 |
3 |
4 |
4.5 |
(1)请画出上表数据的散点图; (2)请根据上表提供的数据,用最小二乘法求出Y关于x的线性回归方程Y=bx+a;(3)已知该厂技改前100吨甲产品的生产能耗为90吨标准煤.试根据(2)求出的线性回归方程,预测生产100吨甲产品的生产能耗比技改前降低多少吨标准煤?
(参考数值:32.5+43+54+64.5=66.5)
设数列{ }是等差数列,数列{
}是等差数列,数列{ }的前
}的前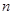 项和
项和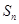 满足
满足 ,
,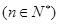 ,且
,且
(1)求数列{ }和{
}和{ }的通项公式:
}的通项公式:
(2)设 为数列{
为数列{ .
. }的前
}的前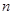 项和,求
项和,求 .
.
火车站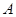 北偏东
北偏东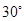 方向的
方向的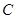 处有一电视塔,火车站正东方向的
处有一电视塔,火车站正东方向的 处有一小汽车,测得
处有一小汽车,测得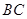 距离为31
距离为31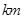 ,该小汽车从
,该小汽车从 处以60公里每小时的速度前往火车站,20分钟后到达
处以60公里每小时的速度前往火车站,20分钟后到达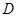 处,测得离电视塔21
处,测得离电视塔21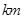 ,问小汽车到火车站还需多长时间?
,问小汽车到火车站还需多长时间?
某企业生产A,B两种产品,生产每吨产品所需的劳动力和煤、电耗如下表:
已知生产每吨A产品的利润是7万元,生产每吨B产品的利润是12万元,现因条件限制,该企业仅有劳动力300个,煤360 t,并且供电局只能供电200 kW,试问该企业生产A,B两种产品各多少吨,才能获得最大利润?
已知 ,
,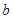 ,
,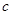 分别为
分别为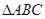 三个内角
三个内角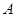 ,
,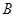 ,
,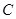 的对边,
的对边, 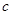 =
=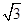
 sin
sin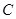
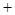
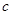 cos
cos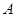 .
.
(1)求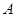 ;
;
(2)若 =
=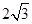 ,
,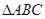 的面积为
的面积为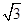 ,求
,求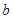 ,
,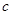 .
.
已知等差数列{ }中,
}中,  (1)求
(1)求 ,
,
(2)设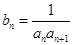 ,求
,求 的前n项和
的前n项和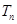 。
。