(本小题满分12分)如图,在三棱锥 中,
中,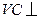 底面
底面 ,
, ,
,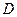 是
是 的中点,且
的中点,且 ,
,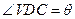
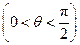 .
.
(1)求证:平面 平面
平面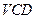 ;(2)当角
;(2)当角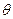 变化时,求直线
变化时,求直线 与平面
与平面 所成的角
所成的角
的取值范围。
(本题9分)
已知函数f(x)=2cosx(sinx-cosx)+1。
(1)求函数f(x)的最小值以及取最小值时x的取值;
(2)求函数f(x)的单调递增区间。
(本题9分)
已知等差数列﹛an﹜满足:a3=1 5, a5+a7=18。
5, a5+a7=18。
(1)求数列﹛an﹜的通项an;
(2)设﹛bn-an﹜是首项为1,公比为3的等比数列,求数列﹛bn﹜的通项公式和前n项和Sn。
(本小题满分12分)已知焦点为 的椭圆经过点
的椭圆经过点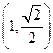 , 直线
, 直线 过点
过点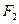 与椭圆交于
与椭圆交于 两点, 其中
两点, 其中 为坐标原点.
为坐标原点.
(1) 求椭圆的方程; (2) 求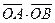 的范围;
的范围;
(3) 若 与向量
与向量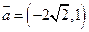 共线, 求
共线, 求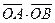 的值及
的值及 的外接圆方程.
的外接圆方程.
(本小题满分12分)已知数列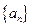 满足
满足
(Ⅰ)求数列 的通项公式;
的通项公式;
(Ⅱ)设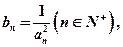 求数列
求数列 的前
的前 项和
项和
(本小题满分12分)已知函数 .
.
(1) 若 在
在 处取得极值, 求
处取得极值, 求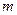 的值;
的值;
(2) 若以函数 图象上任意一点
图象上任意一点 为切点的切线的斜率
为切点的切线的斜率 恒成立, 求正实数
恒成立, 求正实数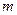 的最小值;
的最小值;
(3) 在(1)的条件下, 若关于 的方程
的方程 在
在 上恰有两个不同的实根, 求实数
上恰有两个不同的实根, 求实数 的取值范围.
的取值范围.