(本小题共13分)已知动圆过定点 ,且与直线
,且与直线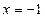 相切.(1)求动圆的圆心轨迹
相切.(1)求动圆的圆心轨迹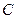 的方程;(2) 是否存在直线
的方程;(2) 是否存在直线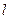 ,使
,使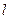 过点(0,1),并与轨迹
过点(0,1),并与轨迹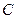 交于
交于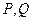 两点,且满足
两点,且满足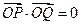 ?若存在,求出直线
?若存在,求出直线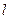 的方程;若不存在,说明理由.
的方程;若不存在,说明理由.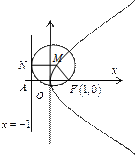
设集合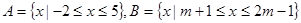 ,
,
(Ⅰ)若 ,求实数
,求实数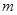 的取值范围;
的取值范围;
(Ⅱ)当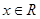 时,没有元素
时,没有元素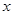 使得
使得 与
与 同时成立,求实数
同时成立,求实数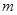 的取值范围.
的取值范围.
现有9名志愿者,其中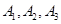 通晓日语,
通晓日语, 通晓英语,
通晓英语,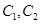 通晓法语,从中选出通晓日语、英语、法语的志愿者各一名,组成一个小组.
通晓法语,从中选出通晓日语、英语、法语的志愿者各一名,组成一个小组.
(Ⅰ)求 至少一个被选中的概率;
至少一个被选中的概率;
(Ⅱ)求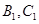 不全被选中的概率.
不全被选中的概率.
(本小题满分14分)设数列 是首项为0的递增数列,
是首项为0的递增数列,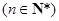 ,
,
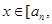
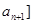 满足:对于任意的
满足:对于任意的 总有两个不同的根. (Ⅰ)试写出
总有两个不同的根. (Ⅰ)试写出 ,并求出
,并求出 ;
;
(Ⅱ)求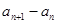 ,并求出
,并求出 的通项公式;
的通项公式;
(Ⅲ)设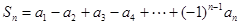 ,求
,求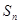 .
.
(本小题满分15分)设 为数列
为数列 的前
的前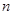 项和,
项和, (
( 为常数且
为常数且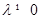 ,
,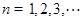 ).
).
(Ⅰ)若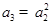 ,求
,求 的值;
的值;
(Ⅱ)对于满足(Ⅰ)中的 ,数列
,数列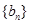 满足
满足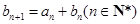 ,且
,且 .若不等式
.若不等式 对任意
对任意 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
(本小题满分15分)在锐角 中,
中, ,
, ,
, 分别为内角
分别为内角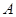 ,
, ,
,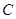 所对的边,且满足
所对的边,且满足 .
.
(Ⅰ)求角 的大小;
的大小;
(Ⅱ)若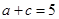 ,且
,且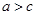 ,
, ,求
,求 的值.
的值.