(本小题满分12分)已知向量 且
且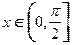 ,(Ⅰ)若
,(Ⅰ)若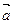 与
与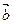 是两个共线向量,求
是两个共线向量,求 的值;
的值;
(Ⅱ)若 ,求函数
,求函数 的最小值及相应的
的最小值及相应的 的值。
的值。
已知条件 ,条件
,条件 ,若
,若 是
是 的充分条件,求实数
的充分条件,求实数 的取值范围.
的取值范围.
已知函数 .
.
(1)求函数 的单调区间;
的单调区间;
(2)当 时,
时, ,求实数
,求实数 的取值范围.
的取值范围.
己知椭圆C: (a>b>0)的右焦点为F(1,0),点A(2,0)在椭圆C上,过F点的直线
(a>b>0)的右焦点为F(1,0),点A(2,0)在椭圆C上,过F点的直线 与椭圆C交于不同两点
与椭圆C交于不同两点 .
.
(1)求椭圆C的方程;
(2)设直线 斜率为1,求线段
斜率为1,求线段 的长;
的长;
(3)设线段 的垂直平分线交
的垂直平分线交 轴于点P(0,y0),求
轴于点P(0,y0),求 的取值范围.
的取值范围.
2015年某市某区高考文科数学成绩抽样统计如下表:
(1)求出表中m、n、M、N的值,并根据表中所给数据在下面给出的坐标系中画出频率分布直方图;(纵坐标保留了小数点后四位小数)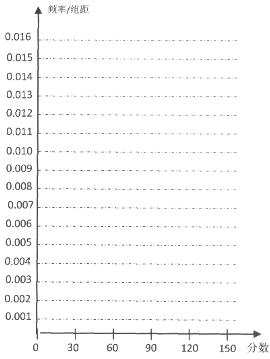
(2)若2015年某市高考文科考生共有20000人,试估计全市文科数学成绩在90分及90分以上的人数;
(3)香港某大学对内地进行自主招生,在参加面试的学生中,有7名学生数学成绩在140分以上,其中男生有4名,要从7名学生中录取2名学生,求其中恰有1名女生被录取的概率.
已知椭圆 :
: ,直线
,直线 交椭圆
交椭圆 于
于 两点.
两点.
(Ⅰ)求椭圆 的焦点坐标及长轴长;
的焦点坐标及长轴长;
(Ⅱ)求以线段 为直径的圆的方程.
为直径的圆的方程.