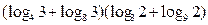某电器商经过多年的经验发现本店每个月售出的电冰箱的台数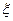 是一个随机变量,它的分布列如下:
是一个随机变量,它的分布列如下:
 |
1 |
2 |
3 |
…… |
12 |
| P |
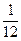 |
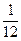 |
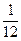 |
…… |
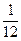 |
设每售出一台电冰箱,电器商获利300元。如销售不出而囤积于仓库,则每台每月需花保养费100元。问电器商每月初购进多少台电冰箱才能使自己月平均收益最大?
定义在 上的函数
上的函数 满足
满足 且当
且当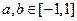 时,
时,
都有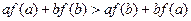 ;
;
(1)判断 在
在 上的单调性,并证明你的结论.
上的单调性,并证明你的结论.
(2)若 是奇函数, 不等式
是奇函数, 不等式 对所有的
对所有的 恒成立,
恒成立,
求 的取值范围.
的取值范围.
随机地把一根长度为8的铁丝截成3段.
(1)若要求三段的长度均为正整数,求恰好截成三角形三边的概率.
(2)若截成任意长度的三段,求恰好截成三角形三边的概率.
某公司对营销人员有如下规定:
①年销售额 在9万元以下,没有奖金,
在9万元以下,没有奖金,
②年销售额 (万元),当
(万元),当 时,奖金为
时,奖金为 (万元),
(万元),
 且年销售额
且年销售额 越大,奖金越多,
越大,奖金越多,
③年销售额超过 81万元,按5﹪ 发奖金(年销售额
发奖金(年销售额 万元).
万元).
(1) 求奖金 关于
关于 的函数解析式;
的函数解析式;
(2)某营销人员争取年奖金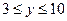 (万元),年销售额
(万元),年销售额 在什么范围内?
在什么范围内?
已知:函数 的定义域是A,函数
的定义域是A,函数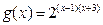
 定义域B
定义域B 的值域是
的值域是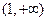 .
.
(1)若不等式 的解集是A,求
的解集是A,求 的值.
的值.
(2)求集合
 (R是实数集).
(R是实数集).
计算下列各式:
(1)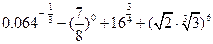
(2)