给定锐角三角形PBC,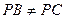 .设A,D分别是边PB,PC上的点,连接AC,BD,相交于点O. 过点O分别作OE⊥AB,OF⊥CD,垂足分别为E,F,线段BC,AD的中点分别为M,N.
.设A,D分别是边PB,PC上的点,连接AC,BD,相交于点O. 过点O分别作OE⊥AB,OF⊥CD,垂足分别为E,F,线段BC,AD的中点分别为M,N.
(1)若A,B,C,D四点共圆,求证: ;
;
(2)若 ,是否一定有A,B,C,D四点共圆?证明你的结论.
,是否一定有A,B,C,D四点共圆?证明你的结论.
设函数 ,p为常数
,p为常数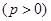 ,
,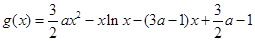 .
.
(1)若对任意的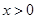 ,恒有
,恒有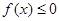 ,求p的取值范围;
,求p的取值范围;
(2)对任意的 ,函数
,函数 恒成立,求实数a的取值范围.
恒成立,求实数a的取值范围.
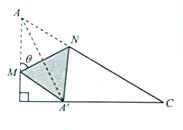
如图,直角三角形ABC中,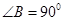 ,
,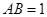 ,
,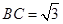 ,点M,N分别在边AB和AC上(M点和B点不重合),将
,点M,N分别在边AB和AC上(M点和B点不重合),将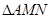 沿MN翻折,
沿MN翻折,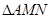 变为
变为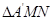 ,使顶点
,使顶点 落在边BC上(
落在边BC上( 点和B点不重合),设
点和B点不重合),设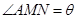 .
.
(1)用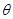 表示线段AM的长度,并写出
表示线段AM的长度,并写出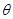 的取值范围;
的取值范围;
(2)求线段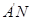 长度的最小值.
长度的最小值.
设函数 (
( 是自然对数的底数).
是自然对数的底数).
(1) 的单调区间、最大值;
的单调区间、最大值;
(2)讨论关于x的方程 根的个数.
根的个数.
设函数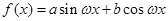
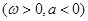 的最小正周期为
的最小正周期为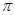 ,
,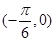 是函数
是函数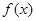 图象的一个对称中心,且曲线
图象的一个对称中心,且曲线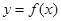 在该点处切线的斜率为
在该点处切线的斜率为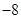 .
.
(1)求a,b,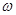 的值;
的值;
(2)若角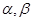 的终边不共线,且
的终边不共线,且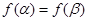 ,求
,求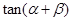 的值;
的值;
(3)若函数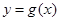 的图象与函数
的图象与函数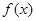 的图象关于直线
的图象关于直线 对称,判断:曲线
对称,判断:曲线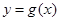 上是否存在与直线
上是否存在与直线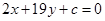 (c为常数)垂直的切线?证明你的结论.
(c为常数)垂直的切线?证明你的结论.
已知函数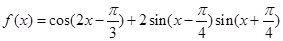 .
.
(1)求函数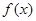 的单调递增区间;
的单调递增区间;
(2)将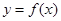 的图象向左平移
的图象向左平移 个单位长度,再将得到的图象横坐标变为原来的2倍(纵坐标不变),得到
个单位长度,再将得到的图象横坐标变为原来的2倍(纵坐标不变),得到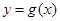 的图象;若函数
的图象;若函数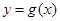 在区间
在区间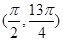 上的图象与直线
上的图象与直线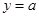 有三个交点,求实数a的取值范围.
有三个交点,求实数a的取值范围.