如图:AD=2,AB=4的长方形 所在平面与正
所在平面与正 所在平面互相垂直,
所在平面互相垂直, 分别为
分别为 的中点.
的中点.
(1)求四棱锥 -
- 的体积;
的体积;
(2)求证: 平面
平面 ;
;
(3)试问:在线段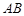 上是否存在一点
上是否存在一点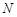 ,使得平面
,使得平面 平面
平面 ?若存在,试指出点
?若存在,试指出点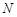 的位置,并证明你的结论;若不存在,请说明理由.
的位置,并证明你的结论;若不存在,请说明理由.
已知直线 :
: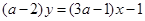
(1)求证:不论实数 取何值,直线
取何值,直线 总经过一定点.
总经过一定点.
(2)为使直线不经过第二象限,求实数 的取值范围.
的取值范围.
(3)若直线 与两坐标轴的正半轴围成的三角形面积最小,求
与两坐标轴的正半轴围成的三角形面积最小,求 的方程.
的方程.
如图,在六面体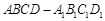 中,
中,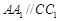 ,
,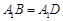 ,
, .
.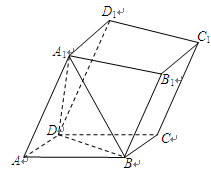
求证:(1) ;(2)
;(2)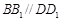 .
.
已知直线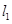 :
: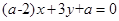 和
和 :
: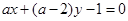 。
。
(1)当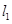 ∥
∥ 时,求a的值(2)当
时,求a的值(2)当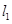 ⊥
⊥ 时求a的值及垂足的坐标
时求a的值及垂足的坐标
如图,在正方体ABCD-A1B1C1D1中,E、F为棱AD、AB的中点.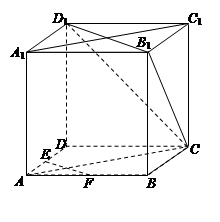
(1)求证:EF∥平面CB1D1;
(2)求证:平面CAA1C1⊥平面CB1D1.