设P(a,b)(b≠0)是平面直角坐标系xOy中的点,l是经过原点与点(1,b)的直线,记Q是直线l与抛物线x2=2py(p≠0)的异于原点的交点
⑴.已知a=1,b=2,p=2,求点Q的坐标。
⑵.已知点P(a,b)(ab≠0)在椭圆+y2=1上,p=,求证:点Q落在双曲线4x2-4y2=1上。
⑶.已知动点P(a,b)满足ab≠0,p=,若点Q始终落在一条关于x轴对称的抛物线上,试问动点P的轨迹落在哪种二次曲线上,并说明理由。
某创业投资公司拟投资开发某种新能源产品,估计能获得10万元到1000万元的投资收益.现准备制定一个对科研课题组的奖励方案:奖金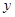 (单位:万元)随投资收益
(单位:万元)随投资收益 (单位:万元)的增加而增加,且奖金不超过9万元,同时奖金不超过投资收益的20%.
(单位:万元)的增加而增加,且奖金不超过9万元,同时奖金不超过投资收益的20%.
(1)若建立函数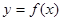 模型制定奖励方案,试用数学语言表述该公司对奖励函数
模型制定奖励方案,试用数学语言表述该公司对奖励函数 模型的基本要求,并分析函数
模型的基本要求,并分析函数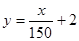 是否符合这个要求,并说明原因;
是否符合这个要求,并说明原因;
(2)若该公司采用函数 作为奖励函数模型,试确定最小的正整数
作为奖励函数模型,试确定最小的正整数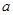 的值.
的值.
如图,在四棱锥 中,底面为直角梯形,
中,底面为直角梯形, ,
, 垂直于底面
垂直于底面 ,
, 分别为
分别为 的中点.
的中点.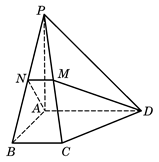
(1)求证: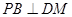 ;
;
(2)求点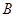 到平面
到平面 的距离.
的距离.
在 中,角
中,角 ,
, ,
, 所对的边分别是
所对的边分别是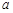 ,
, ,
, ,已知
,已知 ,
, .
.
(1)若 的面积等于
的面积等于 ,求
,求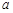 ,
, ;
;
(2)若 ,求
,求 的面积.
的面积.
从某批产品中,有放回地抽取产品二次,每次随机抽取1件,假设事件A“取出的2件产品都是二等品”的概率P(A)=0.04
(1)求从该批产品中任取1件是二等品的概率;
(2)若该批产品共10件,从中任意抽取2件;X表示取出的2件产品中二等品的件数,求X的分布列.
从5名男生和3名女生中任选3人参加奥运会火炬接力活动.若随机变量X表示所选3人中女生的人数,求X的分布表及P(X<2).