汤姆生用来测定电子的比荷(电子的电荷量与质量之比)的实验装置如图所示，真空管内的阴极K发出的电子(不计初速、重力和电子间的相互作用)经加速电压加速后，穿过A'中心的小孔沿中心轴O1O的方向进入到两块水平正对放置的平行极板P和P'间的区域．当极板间不加偏转电压时，电子束打在荧光屏的中心O点处，形成了一个亮点；加上偏转电压U后，亮点偏离到O'点，(O'与O点的竖直间距为d，水平间距可忽略不计．此时，在P和P'间的区域，再加上一个方向垂直于纸面向里的匀强磁场．调节磁场的强弱，当磁感应强度的大小为B时，亮点重新回到O点．已知极板水平方向的长度为L1，极板间距为b，极板右端到荧光屏的距离为L2(如图所示)．
(1)求打在荧光屏O点的电子速度的大小。
(2)推导出电子的比荷的表达式
如图16-4-14所示，半径为R的光滑圆形轨道固定在竖直面内.小球A、B质量分别为m、βm(β为待定系数).A球从左边与圆心等高处由静止开始沿轨道下滑，与静止于轨道最低点的B球相撞，碰撞后A、B球能达到的最大高度均为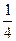
R，碰撞中无机械能损失.重力加速度为g.试求：
图16-4-14
(1)待定系数β；
(2)第一次碰撞刚结束时小球A、B各自的速度和B球对轨道的压力；
(3)小球A、B在轨道最低处第二次碰撞刚结束时各自的速度，并讨论小球A、B在轨道最低处第n次碰撞刚结束时各自的速度.
A、B两滑块在同一光滑的水平直导轨上相向运动发生碰撞(碰撞时间极短).用闪光照相，闪光4次摄得的闪光照片如图16-1-7所示.已知闪光的时间间隔为Δt，而闪光本身持续时间极短.在这4次闪光的瞬间，A、B两滑块均在0—80 cm刻度范围内，且第一次闪光时，滑块A恰好通过x=55 cm处，滑块B恰好通过x=70 cm处.问：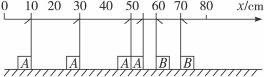
图16-1-7
(1)碰撞发生在何处?
(2)碰撞发生在第一次闪光后多长时间?
如图16-4-13所示，质量均为m的A、B两个弹性小球，用长为2l的不可伸长的轻绳连接，现把A、B两球置于距地面高H处(H足够大)，间距为l，当A球自由下落的同时，将B球以速度v0指向A球水平抛出.求：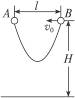
图16-4-13
(1)两球从开始运动到相碰，A球下落的高度；
(2)A、B两球碰撞(碰撞时无机械能损失)后，各自速度的水平分量；
(3)轻绳拉直过程中，B球受到绳子拉力的冲量大小.
如图16-4-10所示，长l为0.8 m的细绳，一端固定于O点，另一端系一个质量m1为0.2 kg的球.将球提起使细绳处于水平位置时无初速释放.当球摆至最低点时，恰与放在光滑水平桌面边缘的质量m2为0.2 kg的铁块发生弹性正碰，碰后小球静止.若光滑桌面距地面高度h为1.25 m，铁块落地点距桌边的水平距离多大？(g取10 m/s2)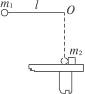
图16-4-10
气球质量
，载有质量为
的人，静止在空中离地
高处，气球下悬一根质量可忽略不计的绳子，一人想从气球上沿绳慢慢滑到地面，为了安全到达地面，这根绳长至少应为（不计人的高度）多长？