物体A质量为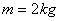 ,用两根轻绳B、C连接到竖直墙上,在物体A上加一恒力F,若图中力F、轻绳AB与水平线夹角均为
,用两根轻绳B、C连接到竖直墙上,在物体A上加一恒力F,若图中力F、轻绳AB与水平线夹角均为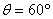 ,要使两绳都能绷直,求恒力F的大小。
,要使两绳都能绷直,求恒力F的大小。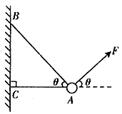
当遇到下大雪时,路面会大量积雪,这时汽车行驶在马路上就会打滑,给交通运输带来极大的影响.高速公路就会封闭.已知汽车橡胶轮胎与普通路面的动摩擦因数为0.7,与积雪路面的动摩擦因数为0.05。当汽车在高速公路上以某一速度沿水平普通路面行驶时,急刹车后(设车轮立即停止转动),汽车要滑行70m才能停下.那么,该汽车若以同样的速度在积雪的水平路面上行驶,求:(取g=10m/s2)
(1)汽车紧急刹车后在积雪的水平路面上滑行的距离是多少?
(2)要使汽车紧急刹车后在积雪的水平路面上70m内停下,汽车行驶的速度不超过多少?
2008年12月,天文学家通过观测的数据确认了银河系中央的黑洞“人马座A*”的质量与太阳质量的关系.研究发现,有一星体S2绕“人马座A*”做椭圆运动,其轨道半长轴为9.50×102个天文单位(地球公转轨道的半径为一个天文单位),“人马座A*”就处在该椭圆的一个焦点上.观测得到S2星的运行周期为15.2年.(计算结果保留一位有效数字)
(1)已知太阳质量Ms=2.0×1030kg,若将S2星的运行轨道视为半径r=9.50×102个天文单位的圆轨道,试估算“人马座A*”的质量MA; (2)理论计算表明,当物体的速度达第一宇宙速度的
(2)理论计算表明,当物体的速度达第一宇宙速度的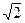 倍时,物体将逃离天体对它的引力,不再绕天体运行.由黑洞理论可知,任何物体即使是光,也不能逃离黑洞.已知G=6.67×10—11N·m2/kg2,c=3.0×108m/s,求黑洞“人马座A*”的最大半径.
倍时,物体将逃离天体对它的引力,不再绕天体运行.由黑洞理论可知,任何物体即使是光,也不能逃离黑洞.已知G=6.67×10—11N·m2/kg2,c=3.0×108m/s,求黑洞“人马座A*”的最大半径.
"凌汛",是黄河等高纬度寒冷地区某些江河特有的自然现象。每年春天,由于黄河上游宁夏地区冰层解冻,解冻的冰凌顺流而下,与内蒙古地区尚未解冻的冰层淤积在一起,形成堵塞河道的冰坝,使得水位大幅度上升,最终漫滩或决堤,造成严重的自然灾害,简称"凌汛".为了清理堵塞河道的冰凌。空军实施投弹爆破.已知飞机在河道上空高
处以某一速度水平匀速飞行,在距冰坝水平距离为
处投弹正好击中目标.求炸弹刚脱离飞 机到击中目标飞行的时间及击中目标时的速度大小.(不计空气阻力)
机到击中目标飞行的时间及击中目标时的速度大小.(不计空气阻力)
如图甲是一种自由电子激光器的原理示意图。经电场加速后的高速电子束,射入上下排列着许多磁铁的管中。相邻两块磁铁的极性是相反的。电子在垂直于磁场的方向上摆动着前进,电子在摆动的过程中发射出光子。管子两端的反射镜(图中未画出)使光子来回反射,光子与自由电子发生相互作用,使光子能量不断增大,从而产生激光输出。
(1)若该激光器发射激光的功率为P = 6.63×10 9 W,激光的频率为υ = 1.0×1016 Hz。则该激光器每秒发出多少个激光光子?(普朗克常量 = 6.63×10-34 J·s)
= 6.63×10-34 J·s)
(2)若加速电压U =1.8×10 4 V,取电子质量 = 9×10-31 kg,电子电荷量e =1.6×10-19C。每对磁极间的磁场可看作匀强磁场,磁感应强度为B = 9×10-4 T。每个磁极的左右宽度为L="30" cm,厚度为2 L 。忽略左右磁极间的缝隙距离,认为电子在磁场中运动的速度大小不变。电子经电场加速后,从上下磁极间缝隙的正中间垂直于磁场方向射入第1对磁极的磁场中,电子一共可通过几对磁极?在图乙的俯视图中,画出电子在磁场中运动轨迹的示意图(尺寸比图甲略有放大)。
= 9×10-31 kg,电子电荷量e =1.6×10-19C。每对磁极间的磁场可看作匀强磁场,磁感应强度为B = 9×10-4 T。每个磁极的左右宽度为L="30" cm,厚度为2 L 。忽略左右磁极间的缝隙距离,认为电子在磁场中运动的速度大小不变。电子经电场加速后,从上下磁极间缝隙的正中间垂直于磁场方向射入第1对磁极的磁场中,电子一共可通过几对磁极?在图乙的俯视图中,画出电子在磁场中运动轨迹的示意图(尺寸比图甲略有放大)。
如图甲所示,空间有Ⅰ区和Ⅲ区两个有理想边界的匀强磁场区域,磁感应强度大小均为B,方向如图所示。两磁场区域之间有宽度为s的无磁场区域Ⅱ。abcd是由均匀电阻丝做成的边长为L(L>s)的正方形线框,每边的电阻为R。线框以垂直磁场边界的速度v水平向右匀速运动,从Ⅰ区经过Ⅱ区完全进入Ⅲ区,线框ab边始终与磁场边界平行。求:
(1)当ab边在Ⅱ区运动时,dc边所受安培力的大小和方向;
(2)线框从完全在Ⅰ区开始到全部进入Ⅲ区的整个运动过程中产生的焦耳热;
(3)请在图乙的坐标图中画出,从ab边刚进入Ⅱ区,到cd边刚进入Ⅲ区的过程中,
d、a两点间的电势差Uda随时间t变化的图线。其中E0 = BLv。