如图所示,半径为R、圆心为O的大圆环固定在竖直平面内,两个轻质小圆环套在大圆环上.一根轻质长绳穿过两个小圆环,它的两端都系上质量为m的重物,忽略小圆环的大小。
(1)将两个小圆环固定在大圆环竖直对称轴的两侧θ=30°的位置上(如图).在-两个小圆环间绳子的中点C处,挂上一个质量M=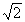 m的重物,使两个小圆环间的绳子水平,然后无初速释放重物M.设绳子与大、小圆环间的摩擦均可忽略,求重物M下降的最大距离.
m的重物,使两个小圆环间的绳子水平,然后无初速释放重物M.设绳子与大、小圆环间的摩擦均可忽略,求重物M下降的最大距离.
(2)若不挂重物M.小圆环可以在大圆环上自由移动,且绳子与大、小圆环间及大、小圆环之间的摩擦均可以忽略,问两个小圆环分别在哪些位置时,系统可处于平衡状态? 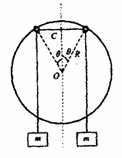
麦克斯韦在1865年发表的《电磁场的动力学理论》一文中揭示丁电、磁现象与光的内在联系及统一性,即光是电磁波。
(1)一单色光波在折射率为l.5的介质中传播,某时刻电场横波图象如图1所示,求该光波的频率。
(2)图2表示两面平行玻璃砖的截面图,一束平行于CD边的单色光入射到AC界面上.a、b 是其中的两条平行光线。光线a在玻璃砖中的光路已给出。画出光线b从玻璃砖中首次出射的光路图,并标出出射光线与界面法线夹角的度数。
某实验室工作人员,用初速度v0 = 2.7×107m/s的α粒子,轰击静止的氮原子核 N,产生了质子
N,产生了质子 H。若某次碰撞可看作对心正碰,碰后新核与质子同方向运动,垂直磁场方向,通过分析偏转半径可得出新核与质子的速度大小之比为1:20,已知质子的质量为m。
H。若某次碰撞可看作对心正碰,碰后新核与质子同方向运动,垂直磁场方向,通过分析偏转半径可得出新核与质子的速度大小之比为1:20,已知质子的质量为m。
(1)写出核反应方程。
(2)求出质子的速度
如图所示:在水平面上放置质量为M=800g的木块,一质量为m=50g的子弹以v0=170m/s的水平速度射入木块,最终与木块一起运动,若木块与地面间的动摩擦因数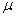 =0.2,求木块在地面上滑行的距离。(g取10m/s2)
=0.2,求木块在地面上滑行的距离。(g取10m/s2)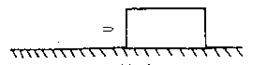
在真空中,原来静止的原子核 在进行
在进行 衰变时,放出
衰变时,放出 粒子的动能为E0。假设衰变后产生的新核用字母Y表示,衰变时产生的能量全部以动能形式释放出来,真空中的光速为c,原子核的质量之比等于质量数之比,原子核的重力不计。
粒子的动能为E0。假设衰变后产生的新核用字母Y表示,衰变时产生的能量全部以动能形式释放出来,真空中的光速为c,原子核的质量之比等于质量数之比,原子核的重力不计。
(1)写出衰变的核反应方程;
(2)求衰变过程中总的质量亏损。
一个运动的处于基态的氢原子与另一个静止的处于基态的氢原子发生完全非弹性碰撞时,可使这两个氢原子发生相同的能级跃迁,则运动的氢原子碰撞前的最小动能是多少?已知氢原子的电离能E=13.6eV.