某商场有奖销售中,购满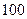 元商品得
元商品得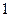 张奖券,多购多得。
张奖券,多购多得。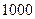 张奖券为一个开奖单位,设特等奖
张奖券为一个开奖单位,设特等奖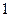 个,一等奖
个,一等奖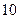 个,二等奖
个,二等奖 个。设
个。设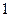 张奖券中特等奖、一等奖、二等奖的事件分别为
张奖券中特等奖、一等奖、二等奖的事件分别为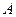 、
、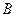 、
、 ,求:
,求:
(1)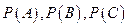 ;
;
(2)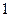 张奖券的中奖概率;
张奖券的中奖概率;
(3)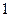 张奖券不中特等奖且不中一等奖的概率。
张奖券不中特等奖且不中一等奖的概率。
如图:直三棱柱油箱底面 的面积是
的面积是 ,
, 、
、 、
、 是三条侧棱上的小孔(其面积忽略不计)
是三条侧棱上的小孔(其面积忽略不计) ,
, ,
, ,若允许油箱倾斜,求这个油箱的最大容积。
,若允许油箱倾斜,求这个油箱的最大容积。
设 ,
,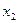 是函数
是函数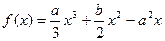 (
(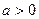 )的两个极值点,且
)的两个极值点,且 .
.
(1)求证: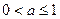 ;(2)求证:
;(2)求证: ;
;
(3)若函数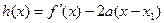 ,求证:当
,求证:当 且
且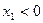 时,
时,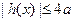 .
.
把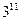 表示成
表示成 个连续正整数的和,求项数
个连续正整数的和,求项数 的最大值.
的最大值.
某校高二年级共有六个班级,现从外地转入4名学生,要安排到该年级的两个班级且每班安排2名,求不同的安排方案种数.
(理)本题共有3个小题,第1小题满分4分,第2小题满分6分,第3小题满分8分.
已知函数 是
是 图像上的两点,横坐标为
图像上的两点,横坐标为 的点
的点 满足
满足 (
( 为坐标原点).
为坐标原点).
(1)求证: 为定值;
为定值;
(2)若
 ,
,
求 的
的 值;
值;
(3)在(2)的条件下,若
 ,
, 为数列
为数列 的前
的前 项和,若
项和,若 对一切
对一切 都成立,试求实数
都成立,试求实数 的取值范围.
的取值范围.