口袋中有质地、大小完全相同的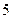 个球,编号分别为
个球,编号分别为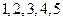 ,甲、乙两人玩一种游戏:甲先摸出一个球,记下编号,放回后乙再摸一个球,记下编号,如果两个编号的和为偶数算甲赢,否则算乙赢.
,甲、乙两人玩一种游戏:甲先摸出一个球,记下编号,放回后乙再摸一个球,记下编号,如果两个编号的和为偶数算甲赢,否则算乙赢.
(1)求甲赢且编号的和为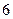 的事件发生的概率;
的事件发生的概率;
(2)这种游戏规则公平吗?试说明理由.
(1) 在直角坐标系xOy中,曲线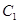 的参数方程为
的参数方程为 为参数),M为
为参数),M为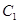 上的动点,P点满足
上的动点,P点满足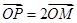 ,点P的轨迹为曲线
,点P的轨迹为曲线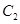 .已知在以O为极点,x轴的正半轴为极轴的极坐标系中,射线
.已知在以O为极点,x轴的正半轴为极轴的极坐标系中,射线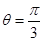 与
与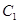 的异于极点的交点为A,与
的异于极点的交点为A,与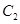 的异于极点的交点为B,求|AB|.
的异于极点的交点为B,求|AB|.
(2) 某旅游景点给游人准备了这样一个游戏,他制作了“迷尼游戏板”:在一块倾斜放置的矩形胶合板上钉着一个形如“等腰三角形”的八行铁钉,钉子之间留有空隙作为通道,自上而下第1行2个铁钉之间有1个空隙,第2行3个铁钉之间有2个空隙,…,第8行9个铁钉之间有8个空隙(如图所示).东方庄家的游戏规则是:游人在迷尼板上方口放人一球,每玩一次(放入一球就算玩一次)先付给庄家2元.若小球到达①②③④号球槽,分别奖4元、2元、0元、-2元.(一个玻璃球的滚动方式:通过第1行的空隙向下滚动,小球碰到第二行居中的铁钉后以相等的概率滚入第2行的左空隙或右空隙.以后小球按类似方式继续往下滚动,落入第8行的某一个空隙后,最后掉入迷尼板下方的相应球槽内).恰逢周末,某同学看了一个小时,留心数了数,有80人次玩.试用你学过的知识分析,这一小时内游戏庄家是赢是赔? 通过计算,你得到什么启示?
规定 =
= ,其中
,其中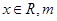 是正整数,且
是正整数,且 =1,这是组合数
=1,这是组合数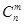 (
(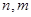 是正整数,且
是正整数,且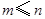 )的一种推广.
)的一种推广.
(1)求 的值;
的值;
(2)设 ,当
,当 为何值时,
为何值时,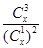 取得最小值?
取得最小值?
(3)组合数的两个性质:①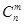 =
=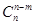 ; ②
; ②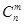 +
+ =
=
是否都能推广到 (
(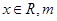 是正整数)的情形?若能推广,则写出推广的形式并给出证明;若不能,则说明理由.
是正整数)的情形?若能推广,则写出推广的形式并给出证明;若不能,则说明理由.
有6本不同的书,按照以下要求处理,各有多少种不同的分法?
(1)一堆一本,一堆两本,一堆三本;
(2)甲得一本,乙得两本,丙得三本;
(3)一人得一本,一人得二本,一人得三本;
(4)平均分给甲、乙、丙三人;
(5)平均分成三堆.
2012年3月2日,江苏卫视推出全新益智答题类节目《一站到底》,甲、乙两人报名参加《一站到底》面试的初试选拔,已知在备选的10道试题中,甲能答对其中的6题,乙能答对其中的8题.规定每次抢答都从备选题中随机抽出3题进行测试,至少答对2题初试才能通过.
(Ⅰ)求甲答对试题数ξ的概率分布及数学期望;
(Ⅱ)求甲、乙两人至少有一人初试通过的概率.
已知 的展开式中,某一项的系数是它前一项系数的2倍,而又等于它后一项系数的
的展开式中,某一项的系数是它前一项系数的2倍,而又等于它后一项系数的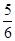
(Ⅰ)求展开后所有项的系数之和及所有项的二项式系数之和;
(Ⅱ)求展开式中的有理项.