如图所示,半径为a的圆形区域内有匀强磁场,磁感应强度B=0.2T,磁场方向垂直纸面向里,半径为b的金属圆环与磁场同心地放置,磁场与环面垂直,其中a=0.4m,b=0.6m,金属环上分别接有灯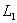 、
、 ,两灯的电阻均为
,两灯的电阻均为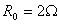 .一金属棒MN与金属环接触良好,棒与环的电阻均不计.
.一金属棒MN与金属环接触良好,棒与环的电阻均不计.
(1)若棒以 的速率在环上向右匀速滑动,求棒滑过圆环直经
的速率在环上向右匀速滑动,求棒滑过圆环直经 的瞬间,MN中的电动势和流过
的瞬间,MN中的电动势和流过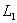 的电流;
的电流;
(2)撤去中间的金属棒MN,将右边的半圆环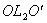 以
以 为轴向上翻转90 ,若此后磁场随时间均匀变化,其变化率为
为轴向上翻转90 ,若此后磁场随时间均匀变化,其变化率为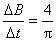 T/s,求
T/s,求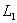 的功率.
的功率.
质量为5000Kg的汽车,在平直公路上以60 kW的恒定功率从静止开始启动,速度达到24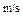 的最大速度后,立即关闭发动机,汽车从启动到最后停下通过的总位移为1200 m.运动过程中汽车所受的阻力不变.求汽车运动的时间.
的最大速度后,立即关闭发动机,汽车从启动到最后停下通过的总位移为1200 m.运动过程中汽车所受的阻力不变.求汽车运动的时间.
如图6-2-13所示,跨过定滑轮的轻绳两端的物体A和B的质量分别为M和m,物体A在水平面上.B由静止释放,当B沿竖直方向下降h时,测得A沿水平面运动的速度为v,这时细绳与水平面的夹角为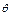 ,试分析计算B下降h过程中,地面摩擦力对A做的功?(滑轮的质量和摩擦均不计)
,试分析计算B下降h过程中,地面摩擦力对A做的功?(滑轮的质量和摩擦均不计)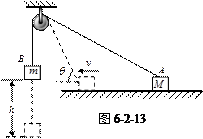
均匀长木板放在水平桌面上如图,厚度不计,它的一端与桌边相齐.已知木板质量为2Kg,长度L=40cm,与桌面间动摩擦因数 .今用水平推力将其推出桌子,问怎样施力可使水平推力做的功最少?最少的功为多大?你能写出几种方案?(g取10m/s2)
.今用水平推力将其推出桌子,问怎样施力可使水平推力做的功最少?最少的功为多大?你能写出几种方案?(g取10m/s2)
一杂技运动员骑摩托车沿一竖直圆轨道做特技表演,如图所示,若车的速度恒为20 m/s,人与车的质量之和为200 kg,摩托车与轨道间的动摩擦因数为μ=0.1,车通过最低点A时,发动机功率为12 kW,求车通过最高点B时发动机的功率(g取10 m/s2).
如图所示为一种加速度仪的示意图。质量为m的振子两端连有劲度系数均为k的轻弹簧,电源的电动势为E,不计内阻,滑动变阻器的总阻值为R,有效长度为L,系统静止时滑动触头位于滑动变阻器正中,这时电压表指针恰好在刻度盘正中。求:
⑴系统的加速度a(以向右为正)和电压表读数U的函数关系式。
⑵将电压表刻度改为加速度刻度后,其刻度是均匀的还是不均匀的?为什么?
⑶若电压表指针指在满刻度的3/4位置,此时系统的加速度大小和方向如何?