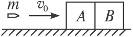
质量为8×107kg的列车,从某处开始进站并关闭动力,只在恒定阻力作用下减速滑行。已知它开始滑行时的初速度为20m/s,当它滑行了300米时,速度减小到10m/s,接着又滑行了一段距离后停止,那么:
(1) 关闭动力时列车的初动能为多大?
(2) 列车受到的恒定阻力为多大?
(3)列车进站滑行的总距离和总时间各为多大?
长1.8 m的细绳悬挂着质量为2 kg的小球,绳的另一端系在离地高3.6 m的天花板上.现将小球从贴着天花板开始自由下落,在细绳被拉直的瞬间绳断裂,接着小球竖直下落到地面上,全过程历时1.2 s.已知小球刚着地时的速度大小为6.5 m/s,不计空气阻力,取g="10" m/s2.求:
(1)细绳刚断裂时小球的速度;
(2)在细绳被拉断的瞬间,绳子受到的平均拉力.
质量m="4" kg的物体静止在水平面上的A点,在F="5" N的水平恒力作用下开始运动,经过一段时间后撤去F,物体运动到B点静止,如图8-2-6所示.已知A、B间距离s="10" m,物体与水平面间的动摩擦因数μ=0.1,求恒力作用在物体上的时间.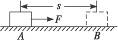
图8-2-6
某消防队员从一平台上跳下,下落2 m后双脚触地,接着他用双腿弯曲的方法缓冲,使自身重心又下降了0.5 m.在着地过程中地面对他双脚的平均作用力估计为其自身重力的多少倍?
一根质量不计、长为1 m、能承受最大拉力为14 N的绳子,一端固定在天花板上,另一端系一质量为1 kg的小球,整个装置处于静止状态,如图所示.若要将绳子拉断,则作用在小球上的水平冲量至少应为多少?(g取10 m/s2)
如图4所示,质量分别为1 kg和2 kg的物体A和B靠在一起静止在光滑水平面上.子弹先后水平射穿A、B分别历时0.01 s及0.02 s,子弹穿行时受到的阻力为300 N.求两物体被射穿后的速度大小.