已知万有引力常量G,地球半径R,地球和月亮之间的距离r,同步卫星距地
面的高度h,月球绕地球运转的周期T1,地球的自转的周期T2,地球表面的重力加速度g。
某同学根据以上条件,提出一种估算地球质量M的方法:同步卫星绕地心作圆周运动,由  。
。
(1)请判断上面的结果是否正确,并说明理由。如不正确,请给出正确的解法和结果。
(2)请根据已知条件再提出两种估算地球质量的方法并解得结果。
一列火车由机车牵引沿水平轨道行使,经过时间t,其速度由0增大到v。已知列车总质量为M,机车功率P保持不变,列车所受阻力f为恒力。求:这段时间内列车通过的路程。
把一根两端开口带有活塞的直管的下端浸入水中,活塞开始时刚好与水面平齐,现将活塞缓慢地提升到离水面H=15m高处,如图7-20所示,求在这过程中外力做功为多少?(已知活塞面积S=1.0dm2,大气压强p0=1.0×105Pa,活塞的厚度和质量不计,取g=10m/s2)
如图7-21所示,A,B两容器容积相同,用细长直导管相连,二者均封入压强为P,温度为T的一定质量的理想气体,现使A内气体温度升温至T',稳定后A容器的压强为多少?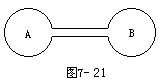
如图7-17所示,一根一端封闭的玻璃管,当L=0.96m,内有一段长h1=0.20m的水银柱。当温度为t1=27℃,开口端竖直向上时,封闭空气柱h2= 0.60m。问温度至少升到多高时,水银柱才能从管中全部溢出?(外界大气压相当于L0= 0.76m高的水银柱产生的压强)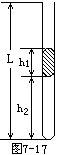
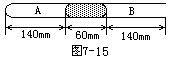
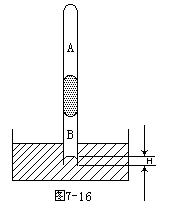
一端封闭一端开口,内径均匀的直玻璃管注入一段60mm的水银柱,当管水平放置达到平衡时,闭端空气柱长140mm,开口端空气柱长140mm,如图7-15所示。若将管轻轻倒转后再竖直插入水银槽内,达到平衡时,管中封闭端空气柱A长133mm,如图7-16所示(设大气压强为1.01325×105Pa(760mmHg),温度保持不变),求槽中水银进入管中的长度H=?