某化工企业生产某种产品,生产每件产品的成本为3元,根据市场调查,预计每件产品的出厂价为x元(7≤x≤10)时,一年的产量为(11 – x)2万件;若该企业所生产的产品能全部销售,则称该企业正常生产;但为了保护环境,用于污染治理的费用与产量成正比,比例系数为常数a (1≤a≤3).
(Ⅰ)求该企业正常生产一年的利润L (x)与出厂价x的函数关系式; 

(Ⅱ)当每件产品的出厂价定为多少元时,企业一年的利润最大,并求最大利润.
(本小题满分12分)设函数 (
(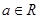 ).
).
(1)当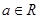 时,讨论函数
时,讨论函数 的单调性;
的单调性;
(2)若对任意 及任意
及任意 ,
, ,恒有
,恒有 成立,求实数
成立,求实数 的取值范围.
的取值范围.
(本小题满分12分)已知函数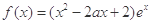 .
.
(Ⅰ)函数 在
在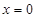 处的切线方程为
处的切线方程为 ,求a、b的值;
,求a、b的值;
(Ⅱ)当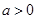 时,若曲线
时,若曲线 上存在三条斜率为k的切线,求实数k的取值范围.
上存在三条斜率为k的切线,求实数k的取值范围.
(本小题满分12分)已知函数
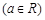 .
.
(1)若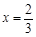 为函数
为函数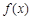 的极值点,求实数
的极值点,求实数 的值;
的值;
(2)若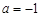 时,方程
时,方程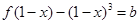 有实数根,求实数
有实数根,求实数 的取值范围.
的取值范围.
(本小题满分12分)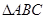 中,角
中,角 的对边分别为
的对边分别为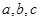 ,已知点
,已知点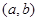 在直线
在直线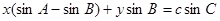 上.
上.
(1)求角 的大小;
的大小;
(2)若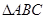 为锐角三角形且满足
为锐角三角形且满足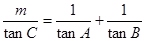 ,求实数
,求实数 的最小值。
的最小值。
(本小题满分10分)已知函数 ,且当
,且当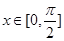 时,
时,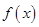 的最小值为2,
的最小值为2,
(1)求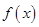 的单调递增区间;
的单调递增区间;
(2)先将函数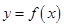 的图象上的点纵坐标不变,横坐标缩小到原来的
的图象上的点纵坐标不变,横坐标缩小到原来的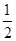 ,再把所得的图象向右平移
,再把所得的图象向右平移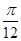 个单位,得到函数
个单位,得到函数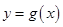 的图象,求方程
的图象,求方程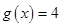 在区间
在区间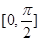 上所有根之和.
上所有根之和.