如图，某客运公司规定旅客可随身携带一定重量的行李，如果超过规定，则需要购买行李票，行李票费用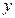
（元）与行李重量
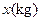的关系用直线
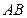的方程表示，试求：
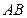（1）直线的方程．
（2）旅客最多可免费携带多少行李？
P是平面ABCD外的点，四边形ABCD是平行四边形，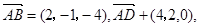
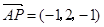,求证
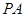垂直平面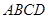
.
设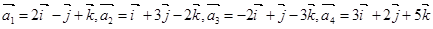
，，试问是否存在实数
，使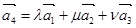
成立？如果存在，求出；如果不存在，请写出证明．
6本不同的书，按照以下要求处理，各有几种分法？
（1）一堆一本，一堆两本，一堆三本；
（2）甲得一本，乙得二本，丙得三本；
（3）平均分给甲、乙、丙三人；
（4）平均分成三堆.
由1，2，3，4，5，6，7的七个数字，试问：
（1）能组成多少个没有重复数字的七位数？
（2）上述七位数中三个偶数排在一起的有几个？
（3）(1)中的七位数中，偶数排在一起、奇数也排在一起的有几个？
（4）(1)中任意两偶然都不相邻的七位数有几个？
直线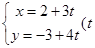
是参数）上两点
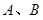对应的参数值分别为
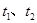，求
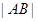的值.