(本小题满分14分)已知 为
为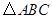 的三个内角
的三个内角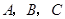 的对边,向量
的对边,向量 ,
,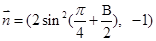 ,
, ,
,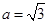 ,
,
(1)求角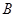 的大小;(2)求
的大小;(2)求 的值.
的值.
某渔业公司年初用98万元购买一艘捕鱼船,第一年各种费用12万元,以后每年都增加4万元,每年捕鱼收益50万元,问:
(1)到第三年扣除购船费用和三年的各种费用,有获利吗?说明理由。
(2)到第几年总的纯收入(扣除购船费用和各年的各种 费用后的收入)达到最大?最大纯收入是多少万元?
费用后的收入)达到最大?最大纯收入是多少万元?
(13分)在 的对边,已知
的对边,已知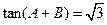 ,
, ,又△ABC的面积
,又△ABC的面积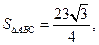
(1)求cosC的值;
(2)求△ABC的周长。
(13分)三棱锥P-ABC中,三条棱PC.AC.BC两两垂直,长都等于2,M为PA的中点,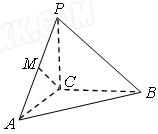
(1)求异面直线CM与AB所成角θ的余弦值;
(2)过点M作一个与平面ABC平行的平面
 ,将此三棱锥截成两部分,分别求这两部分的体积
,将此三棱锥截成两部分,分别求这两部分的体积
(13分)在直角△ABC中AB=4,BC=3,AC=5,将此三角形绕AB边所在直线旋转一周得到一个圆锥
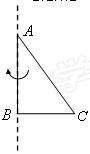
(1)求圆锥的侧面积和体积;
(2)求这个圆锥的内切球的表面积。
海面上相距10海里的A.B两船,B船在A船的北偏东45°方向上,两船同时接到指令同时驶向C岛,C岛在B船的南偏东75°方向上,行驶了80分钟后两船同时到达C岛,经测算,A船行驶了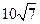 海里,求B船每小时的速度。
海里,求B船每小时的速度。