如图5所示,是自由落体的频闪照片。横线表示小球下落中每隔一个周期所到达的位置。已知频闪周期为0.042s,最下边是第六个位置,标明的数字是28.4,向上依次是19.6和12.5。请你根据这些信息,计算小球经过倒数第2条横线时的速度,以及运动中的加速度。(如果需要估算,重力加速度可取g=10m/s2)
高频焊接是一种常用的焊接方法,其焊接的原理如图所示.将半径为10 cm的待焊接的圆形金属工件放在导线做成的1 000匝线圈中,然后在线圈中通以高频的交变电流,线圈产生垂直于金属工件所在平面的变化磁场,磁场的磁感应强度B的变化率为 πsinωt T/s.焊缝处的接触电阻为工件非焊接部分电阻的99倍.工件非焊接部分每单位长度上的电阻为R0=10-3π Ω·m-1,焊接的缝宽非常小,求焊接过程中焊接处产生的热功率.(取π2=10,不计温度变化对电阻的影响).
πsinωt T/s.焊缝处的接触电阻为工件非焊接部分电阻的99倍.工件非焊接部分每单位长度上的电阻为R0=10-3π Ω·m-1,焊接的缝宽非常小,求焊接过程中焊接处产生的热功率.(取π2=10,不计温度变化对电阻的影响).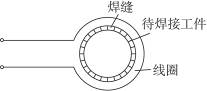
如图所示为一交流发电机构造示意图,n匝矩形线圈abcd,已知ad=L1,ab=L2,匝数为n,线圈abcd以OO′轴在磁感应强度为B的匀强磁场中以角速度ω匀速转动,线圈电阻为r,外电阻为R,求: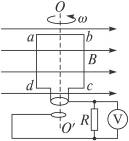
(1)转动过程中电压表的示数;
(2)线圈每转一周,外力所做的功.(不计一切摩擦)
如图所示,单匝线圈在匀强磁场中绕OO′轴从图示位置开始匀速转动,已知从图示位置转过π/6时,线圈中电动势大小为10 V,求: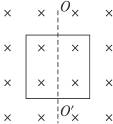
(1)交变电动势的峰值;
(2)交变电动势的有效值;
(3)设线圈电阻为R="1" Ω,角速度ω="100" rad/s,线圈由图示位置转过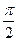 的过程中通过导线截面的电荷量q.
的过程中通过导线截面的电荷量q.
电热毯、电饭锅等是人们常用的电热式家用电器,它们一般具有加热和保温功能,其工作原理大致相同.图17-2-6①为某种电热式电器的简化电路图,主要元件有电阻丝R1、R2和自动开关S.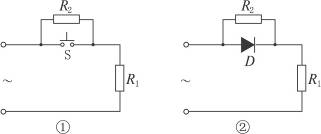
图17-2-6
(1)当自动开关S闭合和断开时,用电器分别处于什么状态?
(2)用电器由照明电路供电(U="220" V),设加热时用电器的电功率为400 W,保温时用电器的电功率为40 W,则R1和R2分别为多大?
(3)若将图①中的自动开关S换成理想的晶体二极管D,如图17-2-6②所示,其他条件不变,求该用电器工作1小时消耗的电能.
一个矩形线圈在一匀强磁场中绕垂直于磁场方向的中心轴匀速转动,产生的交变电动势表达式为e="311sin314t" V,试求:
(1)交变电动势的最大值、有效值和频率;
(2)若矩形线圈是100匝,线圈平面面积为0.02 m2,匀强磁场的磁感应强度B是多少;
(3)当线圈平面从中性面开始转过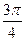 时,电动势的瞬时值是多大.
时,电动势的瞬时值是多大.