动点 到直线
到直线 的距离与它到点
的距离与它到点 的距离之比为
的距离之比为 ,求动点
,求动点 的轨迹方程.
的轨迹方程.
某学生对其30位亲属的饮食习惯进行了一次调查,并用茎叶图表示30人的饮食指数.说明:如图中饮食指数低于70的人,饮食以蔬菜为主;饮食指数高于70的人,饮食以肉类为主.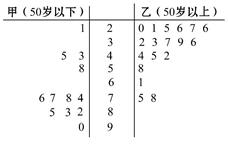
(1)根据茎叶图,帮助这位同学说明其亲属30人的饮食习惯.
(2)根据以上数据完成2×2列联表:
| 主食蔬菜 |
主食肉类 |
总计 |
|
| 50岁以下 |
|||
| 50岁以上 |
|||
| 总计 |
(3)能否在犯错误的概率不超过0.01的前提下认为其亲属的饮食习惯与年龄有关,并写出简要分析.
某制造商3月生产了一批乒乓球,随机抽样100个进行检查,测得每个球的直径(单位:mm),将数据分组如表:
| 分组 |
频数 |
频率 |
 |
| [39.95,39.97) |
10 |
||
| [39.97,39.99) |
20 |
||
| [39.99,40.01) |
50 |
||
| [40.01,40.03] |
20 |
||
| 合计 |
100 |
(1)请在上表中补充完成频率分布表(结果保留两位小数),并在图中画出频率分布直方图.
(2)若以上述频率作为概率,已知标准乒乓球的直径为40.00mm,试求这批乒乓球的直径误差不超过0.03mm的概率.
(3)统计方法中,同一组数据常用该组区间的中点值(例如,区间[39.99,40.01)的中点值是40.00)作为代表.据此估计这批乒乓球直径的平均值(结果保留两位小数).
(·长春模拟)对甲、乙两名自行车赛手在相同条件下进行了6次测试,测得他们的最大速度(m/s)的数据如下表:
| 甲 |
27 |
38 |
30 |
37 |
35 |
31 |
| 乙 |
33 |
29 |
38 |
34 |
28 |
36 |
(1)画出茎叶图.
(2)分别求出甲、乙两名自行车赛手最大速度(m/s)数据的平均数、方差,并判断选谁参加比赛更合适?
如图,已知双曲线C1: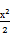 -y2=1,曲线C2:|y|=|x|+1.P是平面内一点.若存在过点P的直线与C1,C2都有共同点,则称P为“C1-C2型点”.
-y2=1,曲线C2:|y|=|x|+1.P是平面内一点.若存在过点P的直线与C1,C2都有共同点,则称P为“C1-C2型点”.
(1)在正确证明C1的左焦点是“C1-C2型点”时,要使用一条过该焦点的直线,试写出一条这样的直线的方程(不要求验证).
(2)设直线y=kx与C2有公共点,求证|k|>1,进而证明原点不是“C1-C2型点”.
(3)求证:圆x2+y2= 内的点都不是“C1-C2型点”.
内的点都不是“C1-C2型点”.
已知点P是圆M:x2+(y+m)2=8(m>0,m≠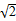 )上一动点,点N(0,m)是圆M所在平面内一定点,线段NP的垂直平分线l与直线MP相交于点Q.
)上一动点,点N(0,m)是圆M所在平面内一定点,线段NP的垂直平分线l与直线MP相交于点Q.
(1)当P在圆M上运动时,记动点Q的轨迹为曲线Г,判断曲线Г为何种曲线,并求出它的标准方程.
(2)过原点斜率为k的直线交曲线Г于A,B两点,其中A在第一象限,且它在x轴上的射影为点C,直线BC交曲线Г于另一点D,记直线AD的斜率为k′,是否存在m,使得对任意的k>0,都有|k·k′|=1?若存在,求m的值;若不存在,请说明理由.