(本小题满分12分)
在如图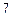 所示的几何体中,
所示的几何体中,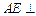 平面
平面 ,
,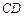 ∥
∥ ,
, 是
是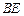 的中点,
的中点,
 ,
, ,
,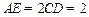 .
.
(Ⅰ)证明 平面
平面 ;
;
(Ⅱ)求二面角 的余弦值.
的余弦值.
图7
本题满分10分)解关于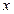 的不等式
的不等式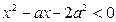
对于函数 ,若存在
,若存在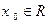 ,使得
,使得 成立,称
成立,称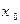 为不动点,已知函数
为不动点,已知函数
(1)当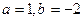 时,求函数
时,求函数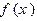 不动点;
不动点;
(2)若对任意的实数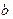 ,函数
,函数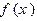 恒有两个相异的不动点,求a的取值范围;
恒有两个相异的不动点,求a的取值范围;
(3)在(2)的条件下,若 图象上A,B两点的横坐标是函数
图象上A,B两点的横坐标是函数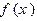 不动点,且
不动点,且 两点关于直线
两点关于直线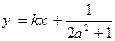 对称,求b的最小值.
对称,求b的最小值.
已知数列 为等差数列,
为等差数列, ,
, ,数列
,数列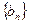 的前
的前 项和为
项和为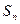 ,且有
,且有
(1)求 、
、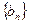 的通项公式;
的通项公式;
(2)若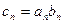 ,
,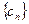 的前
的前 项和为
项和为 ,求
,求 .
.
如图所示,已知 是
是 的外角
的外角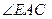 的平分线,交BC的延长线于点D,延长DA交
的平分线,交BC的延长线于点D,延长DA交 的外接圆于点F,连接FB,FC
的外接圆于点F,连接FB,FC
(1)求证: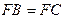
(2)求证: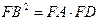
(3)若AB是 外接圆的直径,
外接圆的直径,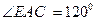
BC=6cm,求AD的长.
过点 作倾斜角为
作倾斜角为 的直线与曲线
的直线与曲线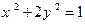 交于点
交于点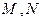 ,求
,求 最小值及相应的
最小值及相应的 值.
值.