如图,已知梯形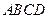 的一底边
的一底边 在平面
在平面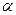 内,另一底边
内,另一底边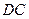 在平面
在平面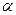 外,对角线交点
外,对角线交点 到平面
到平面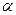 的距离为
的距离为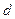 ,若
,若 ,求
,求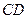 到平面
到平面 的距离.
的距离.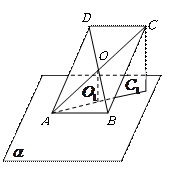
已知命题P:若幂函数 过点
过点 ,实数
,实数 满足
满足 。命题Q:实数
。命题Q:实数 满足
满足 。且
。且 为真,求实数
为真,求实数 的取值范围.
的取值范围.
已知函数 的定义域是
的定义域是 且
且 ,
, ,当
,当 时,
时, .
.
(1)求证: 是奇函数;
是奇函数;
(2)求 在区间
在区间
 )上的解析式;
)上的解析式;
(3)是否存在正整数 ,使得当x∈
,使得当x∈ 时,不等式
时,不等式 有解?证明你的结论.
有解?证明你的结论.
已知抛物线 ,点
,点 ,若斜率为
,若斜率为 的弦过点
的弦过点 ,且以
,且以 为弦中点.
为弦中点.
(1)求抛物线方程;
(2)若 是抛物线过点
是抛物线过点 的任一弦,点
的任一弦,点 是抛物线准线与
是抛物线准线与 轴的交点,直线
轴的交点,直线 分别与抛物线交于
分别与抛物线交于 两点,求证:直线
两点,求证:直线 的斜率为定值,并求
的斜率为定值,并求 的取值范围.
的取值范围.
如图,在平面四边形 中,
中,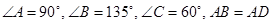 ,
, 分别是边
分别是边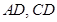 上的点,且
上的点,且 .将
.将 沿对角线
沿对角线 折起,使平面
折起,使平面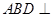 平面
平面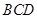 ,并连结
,并连结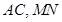 .(如图2)
.(如图2)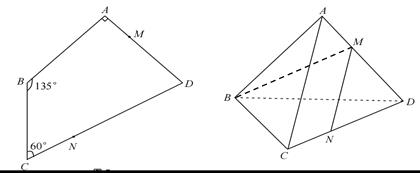
(Ⅰ)证明: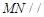 平面
平面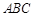 ;
;
(Ⅱ)证明: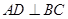 ;(Ⅲ)求直线
;(Ⅲ)求直线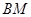 与平面
与平面 所成角的正弦值.
所成角的正弦值.
数列 .
.
(1)
(2)在(1)的结论下,设