已知抛物线 ,点
,点 ,若斜率为
,若斜率为 的弦过点
的弦过点 ,且以
,且以 为弦中点.
为弦中点.
(1)求抛物线方程;
(2)若 是抛物线过点
是抛物线过点 的任一弦,点
的任一弦,点 是抛物线准线与
是抛物线准线与 轴的交点,直线
轴的交点,直线 分别与抛物线交于
分别与抛物线交于 两点,求证:直线
两点,求证:直线 的斜率为定值,并求
的斜率为定值,并求 的取值范围.
的取值范围.
(本小题满分12分)已知直线 :
: 和
和 :
: .问
.问 为何值时,有:
为何值时,有:
(1)
 ?
?
(2) ⊥
⊥ ?
?
(本小题满分14分)设二次函数 满足下列条件:
满足下列条件:
①当 时,其最小值为0,且
时,其最小值为0,且 成立;
成立;
②当 时,
时, 恒成立.
恒成立.
(1)求 的值;
的值;
(2)求 的解析式;
的解析式;
(3)求最大的实数 ,使得存在
,使得存在 ,只要当
,只要当 时,就有
时,就有 成立
成立
(本小题满分13分)已知:函数 对一切实数
对一切实数 都有
都有
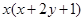 成立,且
成立,且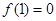 .
.
(1)求 的值;
的值;
(2)求 的解析式;
的解析式;
(3)已知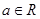 ,设P:当
,设P:当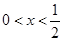 时,不等式
时,不等式 恒成立;Q:当
恒成立;Q:当 时,
时,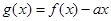 是单调函数。如果满足P成立的
是单调函数。如果满足P成立的 的集合记为
的集合记为 ,满足Q成立的
,满足Q成立的 的集合记为
的集合记为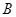 ,求
,求 ∩
∩ (
( 为全集)。
为全集)。
(本小题满分12分)已知函数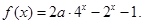
(1)当 时,求函数
时,求函数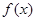 在
在 的值域;
的值域;
(2)若关于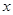 的方程
的方程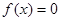 有解,求
有解,求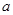 的取值范围
的取值范围
(本小题满分12分)已知函数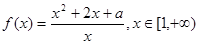 .
.
(1)当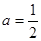 时,求函数
时,求函数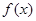 的最小值;
的最小值;
(2)若对任意的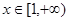 ,
,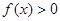 恒成立,试求实数
恒成立,试求实数 的取值范围.
的取值范围.