如图,过椭圆的右焦点作一直线 交椭圆
交椭圆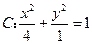 于
于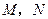 两点,且
两点,且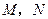 到直线
到直线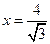 的距离之和为
的距离之和为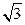 ,求直线
,求直线 的方程.
的方程.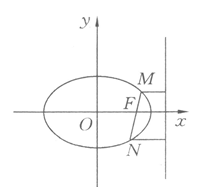

已知幂函数y=f(x)的图象过点(2,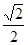 ),试求出此函数的解析式,并写出其定义域,判断奇偶性,单调性.
),试求出此函数的解析式,并写出其定义域,判断奇偶性,单调性.
已知函数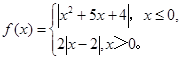 ,若函数
,若函数 恰有4个零点,则实数a的取值范围为.
恰有4个零点,则实数a的取值范围为.
在自然条件下,某草原上野兔第n年年初的数量记为xn,该年的增长量yn和 xn与 的乘积成正比,比例系数为
的乘积成正比,比例系数为 ,其中m是与n无关的常数,且x1<m,
,其中m是与n无关的常数,且x1<m,
(1)证明: ;
;
(2)用 xn表示xn+1;并证明草原上的野兔总数量恒小于m.
如图所示,n台机器人M1,M2,……,Mn位于一条直线上,检测台M在线段M1 Mn上,n台机器人需把各自生产的零件送交M处进行检测,送检程序设定:当Mi把零件送达M处时,Mi+1即刻自动出发送检(i=1,2,……,n-1)已知Mi的送检速度为V(V>0), 且 记
记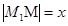 ,n台机器人送检时间总和为f(x).
,n台机器人送检时间总和为f(x).
 |
(1)求f(x)的表达式;
(2)当n=3时,求x的值使得f(x)取得最小值;
(3)求f(x)取得最小值时,x的取值范围.
在等比数列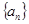 ( n∈N*)中a1>1,公比q>0,设bn=log2an,且b1+b3+b5=6,b1·b3·b5=0.
( n∈N*)中a1>1,公比q>0,设bn=log2an,且b1+b3+b5=6,b1·b3·b5=0.
(1)求证:数列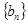 是等差数列;
是等差数列;
(2)求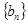 前n项和Sn及
前n项和Sn及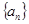 通项an.
通项an.