(本小题共14分)已知函数 其中常数
其中常数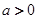 .
.
(1)当 时,求函数
时,求函数 的单调递增区间;
的单调递增区间;
(2)当 时,若函数
时,若函数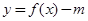 有三个不同的零点,求m的取值范围;
有三个不同的零点,求m的取值范围;
(3)设定义在D上的函数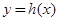 在点
在点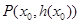 处的切线方程为
处的切线方程为 当
当 时,若
时,若 在D内恒成立,则称P为函数
在D内恒成立,则称P为函数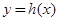 的“类对称点”,请你探究当
的“类对称点”,请你探究当 时,函数
时,函数 是否存在“类对称点”,若存在,请最少求出一个“类对称点”的横坐标;若不存在,说明理由.
是否存在“类对称点”,若存在,请最少求出一个“类对称点”的横坐标;若不存在,说明理由.
已知幂函数 为偶函数,且在区间
为偶函数,且在区间 上是单调减函数(Ⅰ)求函数
上是单调减函数(Ⅰ)求函数 ;(Ⅱ)讨论
;(Ⅱ)讨论 的奇偶性.
的奇偶性.
(Ⅰ)设 是定义在实数集R上的函数,满足
是定义在实数集R上的函数,满足 ,且对任意实数a,b有
,且对任意实数a,b有 求
求 ;
;
(Ⅱ)设函数 满足
满足 求
求
已知函数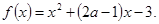
(Ⅰ)当 时,求函数的值域;
时,求函数的值域;
(Ⅱ)若函数 在
在 上的最大值为1,求实数a的值.
上的最大值为1,求实数a的值.
已知集合A={x|3≤x<7},B={x|2<x<10},C={x|5﹣a<x<a}.
(1)求A∪B,(CRA)∩B;
(2)若C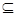 (A∪B),求a的取值范围.
(A∪B),求a的取值范围.
本小题满分12分)设a、b、c成等比数列,非零实数x,y分别是a与b, b与c的等差中项。
(1)已知①a=1、b=2、c=4,试计算 的值;
的值;
②a=-1、b=  、c="-"
、c="-" 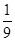 ,试计算
,试计算 的值
的值
(2)试推测 与2的大小关系,并证明你的结论。
与2的大小关系,并证明你的结论。