（本小题满分12分）如图，等腰梯形ABCD的底边AB和CD长分别为6和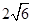
，高为3．
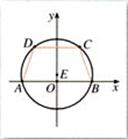
（1）求这个等腰梯形的外接圆E的方程；
（2）若线段MN的端点N的坐标为（5，2），端点M在圆E上运动，求线段MN的中点P的轨迹方程．
已知函数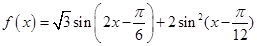
+2m－1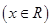
．
（1）求函数
的单调递增区间.
（2）若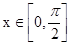
函数取得最小值为5，求m的值．
设命题
：函数
在区间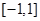
上单调递减；命题
：函数
的定义域是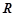
．如果命题
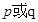为真命题，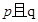
为假命题，求
的取值范围．
在
中，
的对边分别是
，已知
.
（1）求
的值；
（2）若
求的面积
已知集合A={x|x2－3x－10≤0}，集合B={x|p＋1≤x≤2p－1}．若A
B=B，求实数p的取值范围．
已知一个数列
的各项都是1或2．首项为1，且在第
个1和第
个1之间有
个2，即1，2，1，2，2，2，1，2，2，2，2，2，1，…．记数列的前
项的和为
．
参考：31×32=992，32×33＝1056，44×45=1980，45×46=2070，2011×2012＝4046132
（１）试问第2012个1为该数列的第几项？
（２）求
和
；
（３）（特保班做）是否存在正整数
，使得
？如果存在,求出的值；如果不存在,请说明理由．