电子所带电荷量最早是由美国科学家密立根通过油滴实验测出的.油滴实验的原理如图所示,两块水平放置的平行金属板与电源连接,上、下板分别带正、负电荷.油滴从喷雾器喷出后,由于摩擦而带电,油滴进入上板中央小孔后落到匀强电场中,通过显微镜可以观察到油滴的运动情况.两金属板间的距离为d,忽略空气对油滴的浮力和阻力.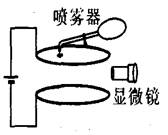
(1)调节两金属板间的电势差U,当u=U0时,使得某个质量为ml的油滴恰好做匀速运动.该油滴所带电荷量q为多少?
(2)若油滴进入电场时的速度可以忽略,当两金属板间的电势差u=U时,观察到某个质量为m2的油滴进入电场后做匀加速运动,经过时间t运动到下极板,求此油滴所带电荷量Q.
一定质量的气体从外界吸收了4.2×105 J的热量,同时气体对外做了6×105 J的功.问:
(1)物体的内能增加还是减少?变化量是多少?
(2)分子势能是增加还是减少?
(3)分子的平均动能是增加还是减少?
在一个标准大气压下,水在沸腾时,1 g的水由液态变成同温度的水蒸气,其体积由1.043 cm3变为1 676 cm3,已知水的汽化热为2 263.8 J/g.求:
(1)体积膨胀时气体对外界做的功W;
(2)气体吸收的热量Q;
(3)气体增加的内能ΔU.
一定质量的气体,在从一个状态变化到另一个状态的过程中,吸收热量280 J,并对外做功120 J,试问:
(1)这些气体的内能发生了怎样的变化?
(2)如果这些气体又返回原来的状态,并放出了240 J热量,那么在返回的过程中是气体对外界做功,还是外界对气体做功?做功多少?
水能不产生污染物,是一种清洁能源,位于美国和加拿大交界处的尼亚加拉瀑布流量可达每秒6 000 m3,而且是一年四季流量稳定,瀑布落差50 m,若利用这一资源发电,设其效率为50%,估算发电机的输出功率.(g取10 m/s2)
如图所示的传动装置中,皮带始终保持v="3" m/s的速度水平匀速前进.m="1" kg的物体无初速地放到皮带上A处,若物体与皮带的动摩擦因数μ=0.15,A、B相距s="4.5" m,问: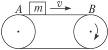
(1)物体从A运动到B需多少时间?(取g="10" m/s2)
(2)物体从A运动到B的过程中,由于摩擦产生的热量为多少?