(1)在“探究恒力做功与动能改变的关系”实验中,某实验小组采用如图甲所示的装置.实验步骤如下:
1把纸带的一端固定在小车的后面,另一端穿过打点计时器
2改变木板的倾角,以重力的一个分力平衡小车及纸带受到的摩擦力
3用细线将木板上的小车通过一个定滑轮与悬吊的砂桶相连
4接通电源,放开小车,让小车拖着纸带运动,打点计时器就在纸带上打下一系列的点
5测出s、s1、s2(如图乙所示),查得打点周期为T.
判断重力的一个分力是否已与小车及纸带受到的摩擦力平衡的直接证据是_______________________________________;
本实验还需直接测量的物理量是:___________________________.(并用相应的符号表示)
探究结果的表达式是______________________________________.(用相应的符号表示)
| 次数 |
小车质量 M/g |
加速度 a/m·s-2 |
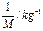 |
| 1 |
200 |
1.91 |
5.00 |
| 2 |
250 |
1.71 |
4.00 |
| 3 |
300 |
1.50 |
3.33 |
| 4 |
350 |
1.36 |
2.86 |
| 5 |
400 |
1.12 |
2.50 |
| 6 |
450 |
1.00 |
2.22 |
| 7 |
500 |
0.90 |
2.00 |
(2)用同样的装置做“探究加速度与力、质量的关系”实验.以下是一实验小组所获取的部分实验数据,根据表格中数据,在图中取合适的坐标系,作出图象.
表格:小车受力相同(均取砂桶质量m=50g).
根据图象判断,实验产生误差的最主要原因是:
________________________________.
一个重力不计的带电粒子,以大小为v的速度从坐标(0,L)的a点,平行于x轴射入磁感应强度大小为B、方向垂直纸面向外的圆形匀强磁场区域,并从x轴上b点射出磁场,射出速度方向与x轴正方向夹角为60°,如图所示.求: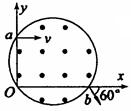
(1)带电粒子在磁场中运动的轨道半径;
(2)带电粒子的比荷q/m及粒子从a点运动到b点的时间;
(3)其他条件不变,要使该粒子恰从O点射出磁场,求粒子入射速度大小.
如图所示的电路中,电源的电动势E="3." 0V,内阻r=1.0Ω;电阻 =10Ω,
=10Ω, 10Ω,
10Ω, =30Ω,
=30Ω, =35Ω;电容器的电容C=100
=35Ω;电容器的电容C=100 .电容器原来不带电,接通电键K.求:
.电容器原来不带电,接通电键K.求:
(1)流过电源的电流;
(2)电阻 两端的电压;
两端的电压;
(3)从接通电键K达到稳定过程中流过 的总电量.
的总电量.
如图所示,在同一水平面的两导轨相互平行,相距2 m并处于竖直向上的匀强磁场中,一根质量为3.6 kg的金属棒放在导轨上,与导轨垂直.当金属棒中的电流为5 A时,金属棒做匀速直线运动,当金属棒中的电流增加到8A时,金属棒将获得2m/s2的加速度(g取10m/s2) 求:
(1)磁场的磁感应强度;
(2)导轨与金属棒间动摩擦因数.
如图所示,水平放置的平行板电容器,原来两板不带电,上极板接地,它的极板长L = 0.1m,两板间距离 d =" 0.4" cm,有一束相同微粒组成的带电粒子流从两板中央平行极板射入,由于重力作用微粒能落到下板上,已知微粒质量为 m = 2×10-6kg,电量q = 1×10-8 C,电容器电容为C =10-6 F.
求 
(1)为使第一粒子能落点范围在下板中点到紧靠边缘的B点之内,则微粒入射速度v0应为多少?
(2)以上述速度入射的带电粒子,最多能有多少个落到下极板上?
在电场中一条电场线上有A、B两点,如图所示.若将一负电荷q=-2.0×10-7C,从A点移至B点,电荷克服电场力做功4.0×10-4J,试求:
(1)电场方向;
(2)A、B两点的电势差多大?哪一点电势高?
(3)在这一过程中,电荷的电势能怎样变化,变化了多少?
(4)如在这一电场中有另一点C,已知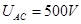 ,若把这一负荷从B移至C电场力做多少功?是正功还是负功?
,若把这一负荷从B移至C电场力做多少功?是正功还是负功?