已知函数 ,
, ,
, ,且
,且 .
.
(1) 求函数 的定义域;
的定义域;
(2) 判断函数 的奇偶性,并说明理由;
的奇偶性,并说明理由;
(3) 求使 成立的
成立的 的集合.
的集合.
(本小题满分14分)设数列 的前
的前 项和为
项和为 ,且对任意的
,且对任意的 都有
都有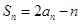 ,
,
(1)求数列 的前三项
的前三项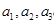 ;
;
(2)猜想数列 的通项公式
的通项公式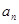 ,并用数学归纳法证明;
,并用数学归纳法证明; (3)求证:对任意
(3)求证:对任意 都有
都有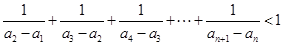 .
.
(本小题满分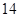 分)如图,在直三棱柱
分)如图,在直三棱柱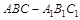 中,
中, 平面
平面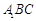 ,其垂足
,其垂足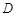 落在直线
落在直线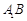 上.
上.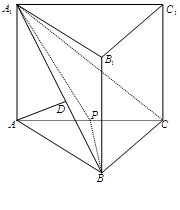
(1)求证: ⊥
⊥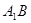
(2)若 ,
,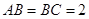 ,
,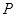 为
为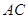 的中点,求二面角
的中点,求二面角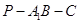 的余弦值.
的余弦值.
(本小题满分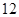 分)为考察高中生的性别与是否喜欢体育课程之间的关系,在我市某普通中学高中生中随机抽取200名学生,得到如下
分)为考察高中生的性别与是否喜欢体育课程之间的关系,在我市某普通中学高中生中随机抽取200名学生,得到如下 列联表:
列联表:
| 喜欢体育课 |
不喜欢体育课 |
合计 |
|
| 男 |
30 |
60 |
90 |
| 女 |
20 |
90 |
110 |
| 合计 |
50 |
150 |
200 |
(1)根据独立性检验的基本思想,约有多大的把握认为“性别与喜欢体育课之间有关系”?
(2)若采用分层抽样的方法从不喜欢体育课的学生中随机抽取5人,则男生和女生抽取的人数分别是多少?
(3)从(2)随机抽取的5人中再随机抽取3人,该3人中女生的人数记为 ,求
,求 的数学期望.
的数学期望.
(本小题满分 分)设函数
分)设函数
(Ⅰ)求f(x)的最小正周期,并指出由f(x)的图象如何变换得到函数y=cos2x的图象;
(Ⅱ)△ABC中角A,B,C的所对边为a,b,c,若f(A﹣ )=
)= ,b=2,c=3,求a的值.
,b=2,c=3,求a的值.
选修4-5;不等式选讲
已知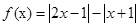
(1)求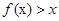 的解集;
的解集;
(2)若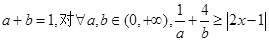 -
-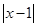 恒成立,求
恒成立,求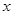 的取值范围.
的取值范围.