(本小题满分12分)在平面上给定非零向量 满足
满足 ,
, 的夹角为600,
的夹角为600,
(1) 试计算 和
和 的值;
的值;
(2) 若向量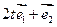 与向量
与向量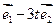 的夹角为钝角,求实数t的取值范围.
的夹角为钝角,求实数t的取值范围.
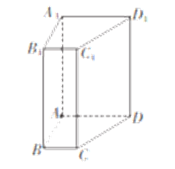
(本小题满分13分)已知四棱柱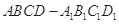 ,侧棱
,侧棱 底面
底面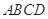 ,底面
,底面 中,
中,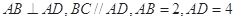 ,侧棱
,侧棱 .
.
(1)若E是 上一点,试确定E点位置使
上一点,试确定E点位置使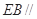 平面
平面 ;
;
(2)在(1)的条件下,求平面BED与平面ABD所成角的余弦值。
(本小题满分12分)已知函数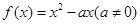 ,
,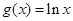 ,
, 图象与
图象与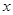 轴异于原点的交点
轴异于原点的交点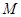 处的切线为
处的切线为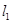 ,
,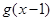 与
与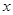 轴的交点
轴的交点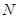 处的切线为
处的切线为 ,并且
,并且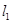 与
与 平行。
平行。
(1)求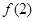 的值;
的值;
(2)已知实数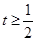 ,求
,求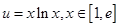 的取值范围及函数
的取值范围及函数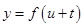 的最值.
的最值.
(本小题满分12分)设函数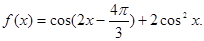
(1)求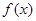 的最大值,并写出使
的最大值,并写出使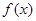 取最大值时
取最大值时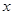 的集合;
的集合;
(2)已知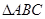 中,角
中,角 的对边分别为
的对边分别为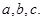 若
若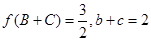 ,求
,求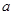 的最小值。
的最小值。
(本小题满分12分)已知命题 ,命题
,命题 的定义域为R,若
的定义域为R,若 ,求实数
,求实数 的取值范围。
的取值范围。
点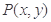 为曲线
为曲线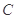 上任一点,点
上任一点,点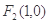 ,直线
,直线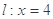 ,点
,点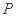 到直线
到直线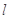 的距离为
的距离为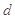 ,且满足
,且满足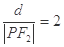 .
.
(1)求曲线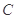 的轨迹方程;
的轨迹方程;
(2)点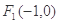 ,点
,点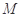 为直线
为直线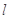 上的一个动点,且直线
上的一个动点,且直线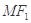 与曲线
与曲线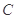 交于两点
交于两点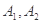 ,直线
,直线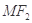 与曲线
与曲线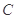 交于两点
交于两点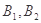 ,求
,求 的取值范围.
的取值范围.