“阳光体育”运动关乎每个学生未来的幸福生活,今年五月,我市某校开展了以“阳光体育我是冠军”为主题的一分钟限时跳绳比赛,要求每个班选2﹣3名选手参赛,现将80名选手比赛成绩(单位:次/分钟)进行统计.绘制成频数分布直方图,如图所示.
(1)图中a值为 .
(2)将跳绳次数在160~190的选手依次记为A1、A2、…An,从中随机抽取两名选手作经验交流,请用树状或列表法求恰好抽取到的选手A1和A2的概率.
如图,一次函数的图象与x轴、y轴分别相交于A、B两点,且与反比例函数 (
( )的图象在第一象限交于点C,如果点B的坐标为(0,2),OA=OB,B是线段AC的中点.
)的图象在第一象限交于点C,如果点B的坐标为(0,2),OA=OB,B是线段AC的中点.
(1)求点A的坐标及一次函数解析式.
(2)求点C的坐标及反比例函数的解析式.
计算: .
.
如图,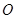 是坐标原点,过点
是坐标原点,过点 的抛物线
的抛物线 与
与 轴的另一个交点为
轴的另一个交点为 ,与
,与 轴交于点
轴交于点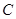 ,其顶点为
,其顶点为 点.
点.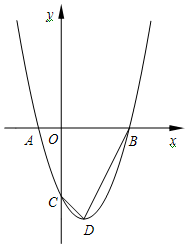
(1)求 的值.
的值.
(2)连结 、
、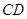 ,动点
,动点 的坐标为
的坐标为 .
.
①当四边形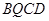 是平行四边形时,求
是平行四边形时,求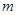 的值;
的值;
②连结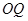 、
、 ,当
,当 最大时,求出点
最大时,求出点 的坐标.
的坐标.
(1)如图1是某个多面体的表面展开图.
①请你写出这个多面体的名称,并指出图中哪三个字母表示多面体的同一点;
②如果沿BC、GH将展开图剪成三块,恰好拼成一个矩形,那么△BMC应满足什么条件?(不必说理)
(2)如果将一个三棱柱的表面展开图剪成四块,恰好拼成一个三角形,如图2,那么该三棱柱的侧面积与表面积的比值是多少?为什么?(注:以上剪拼中所有接缝均忽略不计)