“阳光体育”运动关乎每个学生未来的幸福生活,今年五月,我市某校开展了以“阳光体育我是冠军”为主题的一分钟限时跳绳比赛,要求每个班选2﹣3名选手参赛,现将80名选手比赛成绩(单位:次/分钟)进行统计.绘制成频数分布直方图,如图所示.

(1)图中a值为 .
(2)将跳绳次数在160~190的选手依次记为A1、A2、…An,从中随机抽取两名选手作经验交流,请用树状或列表法求恰好抽取到的选手A1和A2的概率.
如图,已知四棱锥P-ABCD,底面ABCD为菱形,PA1平面ABCD,∠ABC=60°,E,F分别是BC,PC的中点.
(1)证明:AE⊥PD‘
(2)若H为PD上的动点,EH与平面PAD所成最大角的正切值为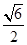 求二面角E-AF-C的余弦值
求二面角E-AF-C的余弦值
某中学在高三开设了4门选修课,每个学生必须且只需选修1门选修课。对于该年级的甲、乙、丙3名学生,回答下面的问题:
(1)求这3名学生选择的选修课互不相同的概率;
(2)某一选修课被这3名学生选修的人数的数学期望.
已知函数以 ,其相邻两个最值点的横坐标之差为2π.
,其相邻两个最值点的横坐标之差为2π.
(1)求f(x)的单调递增区间;
(2)在△ABC中,角A、B、C的对边分别是a、b、c满足(2a-c)cosB=bcosC,求函f(A)的值域.
(本小题满分12分)
已知函数
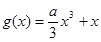 .
.
(1)当 时,求
时,求 的单调区间;
的单调区间;
(2)若 时,不等式
时,不等式 恒成立,求实数
恒成立,求实数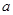 的取值范围.
的取值范围.
(本小题满分12分)
已知函数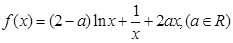
(1)当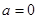 时,求
时,求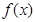 的极值;
的极值;
(2)当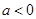 时,求
时,求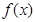 的单调区间.
的单调区间.