如图,已知四棱锥P-ABCD,底面ABCD为菱形,PA1平面ABCD,∠ABC=60°,E,F分别是BC,PC的中点.
(1)证明:AE⊥PD‘
(2)若H为PD上的动点,EH与平面PAD所成最大角的正切值为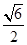 求二面角E-AF-C的余弦值
求二面角E-AF-C的余弦值
(本小题14分) 已知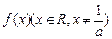 满足ax·f(x)=2bx+f(x), a≠0, f(1)=1且使
满足ax·f(x)=2bx+f(x), a≠0, f(1)=1且使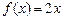 成立的实数x有且只有一个.
成立的实数x有且只有一个.
(1)求 的表达式;
的表达式;
(2)数列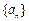 满足:
满足: , 证明:
, 证明: 为等比数列.
为等比数列.
(3)在(2)的条件下, 若 , 求证:
, 求证:
(本小题13分) 如图所示, PQ为平面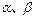 的交线, 已知二面角
的交线, 已知二面角 为直二面角,
为直二面角, 
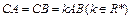 , ∠BAP=45°.
, ∠BAP=45°. 
(1)证明: BC⊥PQ;
(2)设点C在平面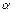 内的射影为点O, 当k取何值时, O在平面ABC内的射影G恰好为△ABC的重心?
内的射影为点O, 当k取何值时, O在平面ABC内的射影G恰好为△ABC的重心?
(3)当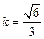 时, 求二面角B-AC-P的大小.
时, 求二面角B-AC-P的大小.
(本小题12分)已知: 以点C (t, )(t∈R , t≠ 0)为圆心的圆与 轴交于点O, A, 与y轴交于点O, B, 其中O为原点.
轴交于点O, A, 与y轴交于点O, B, 其中O为原点.
(1)求证:△OAB的面积为定值;
(2)设直线y = –2x+4与圆C交于点M, N, 若OM = ON, 求圆C的方程.
(本小题12分) 如图,四棱锥P-ABCD的底面是正方形, PA⊥底面ABCD, PA=2,
∠PDA="45°," 点E、F分别为棱AB、PD的中点. 
(1)求证: AF∥平面PCE;
(2)求证: 平面PCE⊥平面PCD;
(3)求AF与平面PCB所成的角的大小.
(本小题12分) 已知两条直线l1: ax-by+4=0和l2: (a-1)x+y+b="0," 求满足下列条件的a, b的值.
(1)l1⊥l2, 且l1过点(-3, -1);
(2)l1∥l2, 且坐标原点到这两条直线的距离相等.