(本小题13分) 如图所示, PQ为平面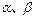 的交线, 已知二面角
的交线, 已知二面角 为直二面角,
为直二面角, 
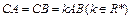 , ∠BAP=45°.
, ∠BAP=45°. 
(1)证明: BC⊥PQ;
(2)设点C在平面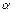 内的射影为点O, 当k取何值时, O在平面ABC内的射影G恰好为△ABC的重心?
内的射影为点O, 当k取何值时, O在平面ABC内的射影G恰好为△ABC的重心?
(3)当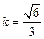 时, 求二面角B-AC-P的大小.
时, 求二面角B-AC-P的大小.
(本小题满分14分)
袋子中有红、白、黄、黑、颜色不同大小相同的四个小球。
(1)从中任取一球,求取出白球的概率。
(2)从中任取两球,求取出的是红球、白球的概率。
(3)从中先后各取一球,求先后取出的分别是红球、白球的概率。
(12分)一汽车厂生产A、B、C三类轿车,每类轿车均有舒适型和标准型两种型号,某月的产量如下表(单位:辆):
| 轿车A |
轿车B |
轿车C |
|
| 舒适型 |
100 |
150 |
z |
| 标准型 |
300 |
450 |
600 |
按类型分层抽样的方法在这个月生产的轿车中抽取50辆,其中有A类轿车10辆.
(1)求z的值;
(2)用分层抽样的方法在C类轿车中抽取一个容量为5的样本。将该样本看成一个总体,从中任取2辆,求至少有1辆舒适型轿车的概率;
(3)用随机抽样的方法从B类舒适型轿车中抽取8辆,经检测它们的得分如下:9.4、8.6、9.2、9.6、8.7、9.3、9.0、8.2,把这8辆轿车的得分看作一个总体,从中任取一个数,求该数与样本平均数之差的绝对值不超过0.5的概率。
(12分) 根据下面的要求,求满足1+2+3+…+n > 500的最小的自然数n。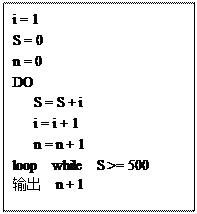
(1)画出执行该问题的程序框图;
(2)以下是解决该问题的一个程序,但有2处错误,请找出错误并予以更正。
若点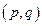 ,在
,在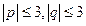 中按均匀分布出现.
中按均匀分布出现.
(1)点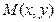 横、纵坐标分别由掷骰子确定,第一次确定横坐标,第二次确定纵坐标,则点
横、纵坐标分别由掷骰子确定,第一次确定横坐标,第二次确定纵坐标,则点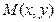 落在上述区域的概率?
落在上述区域的概率?
(2)试求方程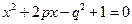 有两个实数根的概率.
有两个实数根的概率.
下面是调查某校学生身高的数据:(单位:cm)
| 分组 |
频数 |
频率 |
| 156.5 ~ 160.5 |
3 |
0.06 |
| 160.5 ~ 164.5 |
4 |
|
| 164.5 ~ 168.5 |
||
| 168.5 ~ 172.5 |
12 |
|
| 172.5 ~ 176.5 |
13 |
0.26 |
| 176.5 ~ 180.5 |
6 |
0.12 |
| 合计 |
1 |
(Ⅰ) 完成上面的表格;根据上表,画出频率分布直方图;
(Ⅱ)根据上表估计,数据在164.5 ~ 176.5 范围内的频率是多少?