(12分)一汽车厂生产A、B、C三类轿车，每类轿车均有舒适型和标准型两种型号，某月的产量如下表(单位:辆)：
| |
轿车A |
轿车B |
轿车C |
| 舒适型 |
100 |
150 |
z |
| 标准型 |
300 |
450 |
600 |
按类型分层抽样的方法在这个月生产的轿车中抽取50辆,其中有A类轿车10辆.
（1）求z的值；
（2）用分层抽样的方法在C类轿车中抽取一个容量为5的样本。将该样本看成一个总体，从中任取2辆，求至少有1辆舒适型轿车的概率；
（3）用随机抽样的方法从B类舒适型轿车中抽取8辆，经检测它们的得分如下：9.4、8.6、9.2、9.6、8.7、9.3、9.0、8.2，把这8辆轿车的得分看作一个总体，从中任取一个数，求该数与样本平均数之差的绝对值不超过0.5的概率。
（本小题12分）
抛物线
上有两个定点A、B分别在对称轴的上、下两侧，F为抛物线的焦点，并且|FA|=2，|FB|=5，（1）求直线AB的方程。
（2）在抛物线AOB这段曲线上求一点P，使△PAB的面积最大，并求这个最大面积.
（本题12分）
设命题p:
,命题
。若
的必要不充分条件，求实数a的取值范围。
（本题12分）
已知中心在原点，一焦点为F（0，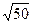
）的椭圆被直线
截得的弦的中点横坐标为
，求此椭圆的方程。
（本题12分）
中心在原点，焦点在x轴
上的一个椭圆与一双曲线有共同的焦点F1,F2,且
,椭圆的长半轴与双曲线的实半轴之差为4，离心率之比为3：7。求这两条曲线的方程.
（本题10分）
求证：△ABC是等边三角形的充要条件是a2＋b2＋c2＝ab＋ac＋bc。这里a、b、c是△ABC的三条边。