(本题12分)
已知中心在原点,一焦点为F(0,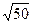 )的椭圆被直线
)的椭圆被直线 截得的弦的中点横坐标为
截得的弦的中点横坐标为 ,求此椭圆的方程。
,求此椭圆的方程。
设函数
的定义域均为
,且
是奇函数,
是偶函数,
,其中
为自然对数的底数.
(Ⅰ)求
的解析式,并证明:当
时,
;
(Ⅱ)设
,证明:当
时,
.
《九章算术》中,将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为阳马,将四个面都为直角三角形的四面体称之为鳖臑. 在如图所示的阳马
中,侧棱
底面
,且
,点
是
的中点,连接
.
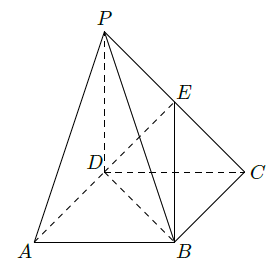
(Ⅰ)证明:
平面
. 试判断四面体
是否为鳖臑,若是,写出其每个面的直角(只需写出结论);若不是,请说明理由;
(Ⅱ)记阳马
的体积为
,四面体
的体积为
,求
的值.
设等差数列
的公差为
,前
项和为
,等比数列
的公比为
.已知
.
(Ⅰ)求数列
,
的通项公式;
(Ⅱ)当
时,记
,求数列
的前
项和
.
某同学用"五点法"画函数
在某一个周期内的图象时,列表并填入了部分数据,如下表:
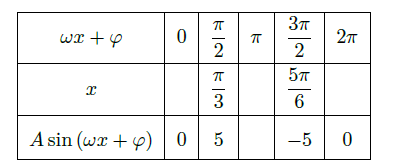
(Ⅰ)请将上表数据补充完整,填写在答题卡上相应位置,并直接写出函数
的解析式;
(Ⅱ)将
图象上所有点向左平行移动
个单位长度,得到
图象,求
的图象离原点
最近的对称中心.
已知数列
的各项均为正数,
,
为自然对数的底数.
(Ⅰ)求函数
的单调区间,并比较
与
的大小;
(Ⅱ)计算
,由此推测计算
的公式,并给出证明;
(Ⅲ)令
,数列
,
的前
项和分别记为
, 证明:
.