(本小题满分14分)已知等差数列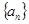 的公差为
的公差为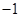 , 且
, 且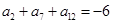 ,
,
(1)求数列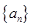 的通项公式
的通项公式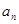 与前
与前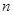 项和
项和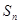 ;
;
(2)将数列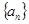 的前
的前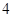 项抽去其中一项后,剩下三项按原来顺序恰为等比数列
项抽去其中一项后,剩下三项按原来顺序恰为等比数列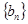 的前3项,记
的前3项,记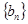 的前
的前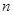 项和为
项和为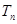 , 若存在
, 若存在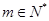 , 使对任意
, 使对任意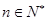 总有
总有 恒成立, 求实数
恒成立, 求实数 的取值范围.
的取值范围.
设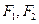 分别是椭圆E:
分别是椭圆E: (a>b>0)的左、右焦点,过
(a>b>0)的左、右焦点,过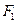 斜率为1的直线l与E 相较于A,B两点,且
斜率为1的直线l与E 相较于A,B两点,且 ,
, ,
, 成等差数列.
成等差数列.
(Ⅰ)求E的离心率;
(Ⅱ)设点P(0,-1)满足 ,求E的方程.
,求E的方程.
为调查某地区老年人是否需要志愿者提供帮助,用简单随机抽样方法从该地区调查了500位老年人,结果如下:
(Ⅰ)估计该地区老年人中,需要志愿者提供帮助的老年人的比例;
(Ⅱ)能否有99%的把握认为该地区的老年人是否需要志愿者提供帮助与性别有关?
(Ⅲ)根据(Ⅱ)的结论,能否提出更好的调查方法来估计该地区的老年人中,需要志愿者提供帮助的老年人的比例?说明理由.

如图,己知四棱锥P-ABCD的底面为等腰梯形,AB∥CD, ⊥BD垂足为H,PH是四棱锥的高,E为AD中点.
⊥BD垂足为H,PH是四棱锥的高,E为AD中点. 
(Ⅰ)证明:PE⊥BC
(Ⅱ)若 =
=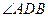 =60°,求直线PA与平面PEH所成角的正弦值.
=60°,求直线PA与平面PEH所成角的正弦值.
设数列 满足
满足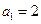 ,
,
(Ⅰ)求数列 的通项公式:
的通项公式:
(Ⅱ)令 ,求数列
,求数列 的前n项和
的前n项和 .
.
(本小题满分10分)选修4—5;不等式选讲
设函数f(x)=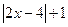
(Ⅰ)画出函数y=f(x)的图像;
(Ⅱ)若不等式f(x)≤ax的解集非空,求a的取值范围.