(本小题满分14分)
袋子中有红、白、黄、黑、颜色不同大小相同的四个小球。
(1)从中任取一球,求取出白球的概率。
(2)从中任取两球,求取出的是红球、白球的概率。
(3)从中先后各取一球,求先后取出的分别是红球、白球的概率。
已知函数
(I)求不等式 的解集;
的解集;
(II)若关于x的不等式 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
以直角坐标系的原点O为极点,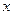 轴的正半轴为极轴,且两个坐标系取相等的单位长度.已知直线l经过点P(1,1),倾斜角
轴的正半轴为极轴,且两个坐标系取相等的单位长度.已知直线l经过点P(1,1),倾斜角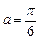 .
.
(I)写出直线l的参数方程;
(II)设l与圆 相交于两点A、B,求点P到A、B两点的距离之积.
相交于两点A、B,求点P到A、B两点的距离之积.
如图,在△ 中,
中, 是
是 的中点,
的中点, 是
是 的中点,
的中点, 的延长线交
的延长线交 于
于 .
.
(Ⅰ)求 的值;
的值;
(Ⅱ)若△ 的面积为
的面积为 ,四边形
,四边形 的面积为
的面积为 ,求
,求 的值.
的值.
设函数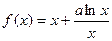 ,其中
,其中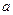 为常数.
为常数.
(Ⅰ)证明:对任意 ,
, 的图象恒过定点;
的图象恒过定点;
(Ⅱ)当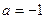 时,判断函数
时,判断函数 是否存在极值?若存在,求出极值;若不存在,说明理由;
是否存在极值?若存在,求出极值;若不存在,说明理由;
(Ⅲ)若对任意 时,
时, 恒为定义域上的增函数,求
恒为定义域上的增函数,求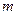 的最大值.
的最大值.
请考生在第22、23、24题中任选一题做答,如果多做,则按所做的第一题记分.
已知椭圆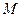 的对称轴为坐标轴,且抛物线
的对称轴为坐标轴,且抛物线 的焦点是椭圆
的焦点是椭圆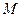 的一个焦点,又点
的一个焦点,又点
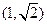 在椭圆
在椭圆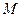 上.
上.
(Ⅰ)求椭圆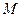 的方程;
的方程;
(Ⅱ)已知直线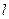 的方向向量为
的方向向量为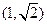 ,若直线
,若直线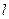 与椭圆
与椭圆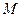 交于
交于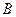 、
、 两点,求
两点,求 面积的最大值.
面积的最大值.