设函数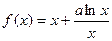 ,其中
,其中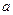 为常数.
为常数.
(Ⅰ)证明:对任意 ,
, 的图象恒过定点;
的图象恒过定点;
(Ⅱ)当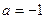 时,判断函数
时,判断函数 是否存在极值?若存在,求出极值;若不存在,说明理由;
是否存在极值?若存在,求出极值;若不存在,说明理由;
(Ⅲ)若对任意 时,
时, 恒为定义域上的增函数,求
恒为定义域上的增函数,求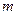 的最大值.
的最大值.
请考生在第22、23、24题中任选一题做答,如果多做,则按所做的第一题记分.
(本小题满分14分)设正项数列 的前
的前 项和
项和 满足
满足 .
.
(Ⅰ)求数列 的通项公式;
的通项公式;
(Ⅱ)令 ,数列
,数列 的前
的前 项和为
项和为 ,证明:对于任意
,证明:对于任意 ,都有
,都有  .
.
(本小题满分13分)在如图的几何体中,平面 为正方形,平面
为正方形,平面 为等腰梯形,
为等腰梯形, ∥
∥ ,
, ,
, ,
, .
.
(Ⅰ)求证: 平面
平面 ;
;
(Ⅱ)求直线 与平面
与平面 所成角的正弦值.
所成角的正弦值.
(本小题满分13分)已知 、
、 、
、 分别为
分别为 的三边
的三边 、
、 、
、 所对的角,
所对的角, 的面积为
的面积为 ,且
,且 .
.
(Ⅰ)求角 的大小;
的大小;
(Ⅱ)若 ,求
,求 周长的最大值.
周长的最大值.
已知偶函数 (
( )在点
)在点 处的切线与直线
处的切线与直线 垂直,函数
垂直,函数 .
.
(Ⅰ)求函数 的解析式.
的解析式.
(Ⅱ)当 时,求函数
时,求函数 的单调区间和极值点;
的单调区间和极值点;
(Ⅲ)证明:对于任意实数x,不等式 恒成立.(其中e=2.71828…是自然对数的底数)
恒成立.(其中e=2.71828…是自然对数的底数)
已知 中,点
中,点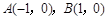 ,动点
,动点 满足
满足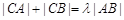 (常数
(常数 ),
), 点的轨迹为Γ.
点的轨迹为Γ.
(Ⅰ)试求曲线Γ的轨迹方程;
(Ⅱ)当 时,过定点
时,过定点 的直线与曲线Γ相交于
的直线与曲线Γ相交于 两点,
两点, 是曲线Γ上不同于
是曲线Γ上不同于 的动点,试求
的动点,试求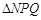 面积的最大值.
面积的最大值.