已知椭圆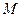 的对称轴为坐标轴,且抛物线
的对称轴为坐标轴,且抛物线 的焦点是椭圆
的焦点是椭圆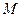 的一个焦点,又点
的一个焦点,又点
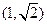 在椭圆
在椭圆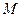 上.
上.
(Ⅰ)求椭圆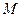 的方程;
的方程;
(Ⅱ)已知直线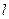 的方向向量为
的方向向量为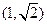 ,若直线
,若直线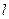 与椭圆
与椭圆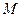 交于
交于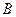 、
、 两点,求
两点,求 面积的最大值.
面积的最大值.
某种产品的广告费用支出 与销售额
与销售额 之间有如下的对应数据:
之间有如下的对应数据:
(1)画出散点图;并说明销售额y与广告费用支出x之间是正相关还
是负相关?
 |
2 |
4 |
5 |
6 |
8 |
 |
30 |
40 |
60 |
50 |
70 |
(2)请根据上表提供的数据,用最小二乘法求出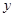 关于
关于 的线性回归方程
的线性回归方程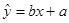 ;(其中:
;(其中: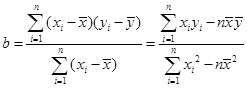 ,
, 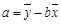 )求回归直线方程.
)求回归直线方程.
(3)据此估计广告费用为10时,销售收入 的值
的值
函数f(x)= 4x3+ax2+bx+5的图在x=1处的切线方程为 ;
;
(1)求函数f(x)的解析式;
(2)求函数f(x)在 [—3,1]上的最值.
已知圆C的参数方程为 (
( 为参数),P是圆C与x轴的正半轴的交点.
为参数),P是圆C与x轴的正半轴的交点.
(Ⅰ)求过点P的圆C的切线方程;
(Ⅱ)在圆C上求一点Q(a, b),它到直线x+y+3=0的距离最长,并求出最长距离.
设
(1)计算: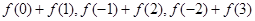 的值;
的值;
(2)猜想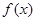 具备的一个性质,并证明.
具备的一个性质,并证明.
已知p:x < -2,或x > 10;q: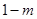 ≤x≤
≤x≤ ;¬p是q的充分而不必要条件,求实数
;¬p是q的充分而不必要条件,求实数 的取值范围.
的取值范围.