如图所示。水平传送装置由轮半径均为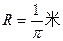 的主动轮O1和从动轮O2及传送带等构成。两轮轴心相距L=8.0米,轮与传送带不打滑。现用此装置运送一袋面粉,已知面粉袋与传送带间的动摩擦因数为μ=0.4,这袋面粉中间的面粉可不断地从袋中渗出。
的主动轮O1和从动轮O2及传送带等构成。两轮轴心相距L=8.0米,轮与传送带不打滑。现用此装置运送一袋面粉,已知面粉袋与传送带间的动摩擦因数为μ=0.4,这袋面粉中间的面粉可不断地从袋中渗出。
(1)当传送带以v0==4.0m/s的速度匀速运动时,将这袋面粉由左端O2正上方的A点轻放在传送带上后,这袋面粉由A端运送到O1正上方的B端所用时间为多少?
(2)要想尽快将这带面粉由A端送到B端(设初速度仍为零),传送带的速度至少应为多大?
(3)由于面粉的渗漏,在运送这袋面粉的过程中会在深色传送带上留下白色的面粉的痕迹。这袋面粉在传送带上留下的痕迹最长能有多长(设袋的初速度仍为零)?此时传送带的速度至少应为多大?
航天飞机,可将物资运送到空间站,也可维修空间站出现的故障。
(1)若已知地球半径为R,地球表现重力加速度为g,某次维修作业中,与空间站对接的航天飞机的速度计显示飞机的速度为v,则该空间站轨道半径R′为多大?
(2)为完成某种空间探测任务,在空间站上发射的探测器通过向后喷气而获得反冲力使其启动。已知探测器的质量为M,每秒钟喷出的气体质量为m,为了简化问题,设喷射时探测器对气体做功的功率恒为P,在不长的时间内探测器的质量变化较小,可以忽略不计。求喷气t秒后探测器获得的动能是多少?
如图所示,匀强电场方向沿
轴的正方向,场强为
。在 点有一个静止的中性微粒,由于内部作用,某一时
点有一个静止的中性微粒,由于内部作用,某一时 刻突然分裂成两个质量均为
的带电微粒,其中电荷量为
刻突然分裂成两个质量均为
的带电微粒,其中电荷量为
 的微粒1沿
轴负方向运动,经过一段时间到达
点。
的微粒1沿
轴负方向运动,经过一段时间到达
点。 不计重力和分裂后两微粒间的作用。试求
不计重力和分裂后两微粒间的作用。试求 (1)分裂时两个微粒各自的速度;
(1)分裂时两个微粒各自的速度; (2)当微粒1到达
点时,电场力对微粒1做功的
(2)当微粒1到达
点时,电场力对微粒1做功的 瞬间功率;
瞬间功率; (3)当微粒1到达
点时,两微粒间的距离。
(3)当微粒1到达
点时,两微粒间的距离。
在如图所示的水平导轨上(摩擦、电阻忽略不计),有竖直向下的匀强磁场,磁感强度B,导轨左端的间距为L1=4l0,右端间距为l2=l0。今在导轨上放置ACDE两根导体棒,质量分别为m1=2m0,m2=m0,电阻R1=4R0,R2=R0。若AC棒以初速度V0向右运动,求AC棒运动的过程中产生的总焦耳热QAC,以及通过它们的总电量q。
如图所示,质量为1g的小环带4×10-4C的正电荷,套在长直的绝缘杆上,两者间的动摩擦因数μ=O.2。将杆放入都是水平的互相垂直的匀强电场和匀强磁场中,杆所在平面与磁场垂直,杆与电场的夹角为37°。若E=10N/C,B=O.5T,小环从静止起动。求:
(1)当小环加速度最大时,环的速度和加速度;
(2)当小环的速度最大时,环的速度和加速度。
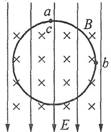
如图所示,在某空间同时存在着互相正交的匀强电场和匀强磁场,电场的方向竖直向下。一带电体a带负电荷,电量为q1,恰能静止于此空间的c点,另一带电体b也带负电荷,电量为q2,正在过a点的竖直平面内作半径为R的匀速圆周运动,结果a、b在c处碰撞并粘合在一起,试分析a、b粘合一起后的运动性质。